Recuerdo un viaje a Chicago, hace unos años. Estábamos a punto de aterrizar cuando el capitán nos avisó, como el que no quiere la cosa, de que llevábamos un avión al lado. Menos mal que viajaba en una línea aérea norteamericana y no en Iberia. No dudo de la competencia de los pilotos nacionales, pero suelen ser un poco estirados cuando se trata de dirigirse al pasaje y nada como un tipo estirado para darte un susto si algo se sale de lo normal. En cambio, aquel piloto (tejano, por el acento) nos hablaba como si fuera el guía de una excursión a Benidorm. “Hi folks” (o sea, hola tíos) empezó, “Mirad por la ventanilla izquierda, veréis qué divertido”. La diversión era un Boeing aterrizando en paralelo al nuestro y la impresión subjetiva es que estaba a dos palmos de nosotros. El susto fue morrocotudo, pero lo hubiera sido aún más de no ser por la cachaza conque el capitán nos contaba, tan colega él, la película. “Como veis el aeropuerto está de bote en bote, mucho tráfico aéreo, pero no os preocupéis: esto lo hacemos todos los días…”, etcétera, etcétera, el hombre no paraba de hablar. El caso es que el mensaje era bien breve: que nadie se asuste, enseguida aterrizamos. Para concluir nos dijo: just normal operations, folks, just normal operations.
Bueno, en esta entrega también vamos a hacer un par de operaciones, en este caso algebraicas, para deducir de manera muy sencilla cómo relacionar el valor del factor de dilatación temporal relativista. Que nadie se asuste, por favor, se trata de unas cuentas la mar de sencillas. Sólo necesitamos saber dos cosas:
1. El teorema de Pitágoras que relaciona la hipotenusa de un triángulo rectángulo con sus catetos:
h² = x² + y²
Donde h es la hipotenusa del triángulo y x, y los dos catetos.
2. La relación entre velocidad, espacio y tiempo:
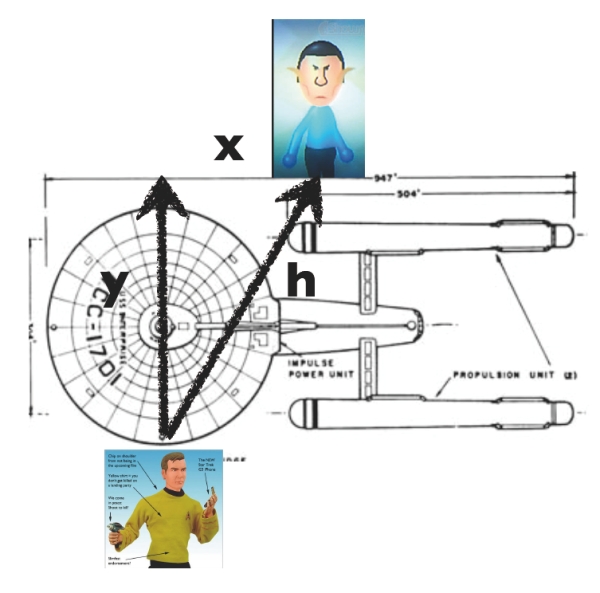
Si miramos por la ventanilla de nuestro Gedankenexperiment veremos la Enterprise, tal como la dejamos en la entrega anterior. En la figura, y es la distancia que recorre la luz en el sistema de referencia de Kirk; x es la distancia que recorre la Enterprise; h es la distancia que recorre la luz en el sistema de referencia de Spock.
Pero si v = e/t, entonces e = v · t, es decir la distancia y no es más que la velocidad (de la luz) multiplicada por el tiempo (medido en el sistema de referencia de Kirk). Entonces:
![]() y si elevamos todo al cuadrado:
y si elevamos todo al cuadrado:
![]() Donde c como siempre es la velocidad de la luz.
Donde c como siempre es la velocidad de la luz.
Por otra parte la distancia x es la velocidad de la nave multiplicada por el tiempo medido en el sistema de referencia de Spock. Entonces:
y elevando de nuevo al cuadrado:
Donde v es la velocidad de la Enterprise.
Finalmente, la hipotenusa es la distancia que la luz recorre en el sistema de referencia de Spock.
o sea:
La relación entre las tres distancias viene dada por el teorema de Pitágoras, h² = x² + y². Despejando:
y² = h² – x²
Esto es lo mismo que escribir:
Si ahora dividimos a izquierda y derecha de la ecuación por c², nos sale:
Una pizca de álgebra:
Ya casi hemos aterrizado. Sólo nos falta introducir un par de letras griegas (un truco que utilizan los físicos para hacerse los importantes). Una de ellas, β, denomina la velocidad de un objeto con respecto a la velocidad de la luz.
La luz, lógicamente, se mueve a β = 1. Un AVE, por ejemplo, se mueve a:
Un avión comercial, como el Boeing que nos llevaba a Chicago vuela a unos 1000 km/h, así que su b vale 0.0009, o, en números redondos un uno por mil de la velocidad de la luz. Comparado con c todos nuestros vehículos se mueven a la velocidad de la tortuga.
Si llamamos, para simplificar la notación t al tiempo de Kirk y t0 al tiempo de Spock (t mide el tiempo del observadorque se mueve con velocidad v —o β— y t0 el del observador en reposo), nos queda:
Y si sacamos la raíz cuadrada:
¿Qué pasa cuando viajamos a velocidades pequeñas comparadas con las de la luz (por ejemplo en un AVE o en Boeing)? En ese caso β ˜ 0 y por lo tanto t = t0. El tiempo del pasajero en el avión es el mismo que el tiempo del familiar que le espera en Chicago (aunque, viendo al otro avión a un palmo de su ala mientras aterriza, al viajero su tiempo se le hace larguísimo).
¿Y si viajamos exactamente a la velocidad de la luz? Pues si v = c, entonces β = 1 y t = 0, independientemente de lo que valga (t0), lo que quiere decir que a la velocidad de la luz, el tiempo detiene.
En la entrega anterior vimos que la Enterprise iba a β = 0,6. En ese caso ya se empiezan a notar los efectos relativistas:
Esto es, por cada diez años de Spock, pasan 8 años de Kirk.
La segunda letra griega que nos conviene introducir se llama γ y vale:
Lo que nos permite escribir la fórmula de dilatación temporal de una forma muy elegante:
A γ le llamamos factor de dilatación temporal. Cuanto más se acerca β a uno, mas pequeño es el término √1 – β ², y más grande γ que es la inversa de ese término. Cuanto mayor la dilatación temporal más lento el tiempo de Kirk respecto al tiempo de Spock. Para: ![]()
En la próxima entrega veremos cómo aumenta la dilatación temporal a medida que nos acercamos a la velocidad de la luz y cómo eso influye en los viajes espaciales.



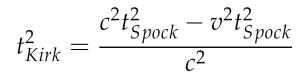








Lo de que a la velocidad de la luz el tiempo se detenga, ese punto límite, me plantea varias preguntas: ¿la luz, por lo tanto, no viaja en el tiempo al ser siempre su tiempo 0? Si la respuesta a esa pregunta es sí, ¿cómo entonces puede tener «velocidad»? ¿entonces a la luz le falta una dimensión en «nuestro» universo en el que sí existe el tiempo? ¿el tiempo de vida de un fotón es infinito? y ya relacionando esto con aquella pregunta del Piz(z)ero, ¿qué pasa cuando chocan dos fotones en la misma dirección y sentido contrario? y el caso opuesto ¿qué tiempo se mide entre dos fotones que se alejan el uno del otro en el mismo eje?
Hola,
Muy agudos comentarios,
El problema aqui es el concepto de tiempo como una cantidad separada del espacio. La relatividad nos permite formular el movimiento (y la dinamica) de los objetos en terminos de vectors con cuatro coordenadas (x,y,z,t). De ahi que podamos imaginarnos un universo curiosamente «estatico» en el que todo ha sucedido (si miras a lo largo de la coordenada t). En ese espacio no tiene nada de particular que el tiempo no pase en el sistema de referencia del foton de luz, como no tiene nada de particular que alguien este parado y sus coordenadas espaciales sean fijas.
tu pregunta: «a la luz le falta una dimension en neustro universo en que existe el tiempo?» va en la direccion correcta: en el espacio (x,y,z,t) la luz no se mueve a lo largo de t. Y como ya te imaginas, el tiempo relativo entre dos fotones que se alejan uno de otro en el mismo eje es cero. Si los dos se emiten a la vez, llegan al detector a la vez.
Dos particulas elementales (electrones, fotones, protones) que chocan entre si pueden aniquilarse produciendo un estado puro de energia (E=mc2) que despues se «condensa» de nuevo en otras particulas. Igual que es posible que un pi0 se desintege a 2 fotones, cuando dos fotones se aniquilan pueden producir 2 piones. De todo eso hablaremos mas pronto…
Gracias!
J
Pingback: Juan José Gómez Cadenas: Normal operations
Me he planteado un Gedankenexperiment con balas disparadas desde un tren y llego a una paradoja.
En el centro del tren hay dos pistolas apuntando en sentidos opuestos. Cuando el tren está parado, al dispararse las pistolas a la vez, las balas salen a 300 m/s hacia delante y atrás. Hay dos dianas a 900 m de las pistolas. Ambas balas llegan a las dianas al mismo tiempo, 3 segundos.
Para una persona dentro del tren las balas se mueven a 300 m/s.
Para una persona en el andén las balas se mueven también a 300 m/s.
Ahora el tren se mueve a 300 m/s en uno de los sentidos. Se disparan las balas.
Para la persona dentro del tren las balas siguen moviéndose a 300m/s.
¿A qué velocidad se mueven las balas para la persona en el andén?. ¿La bala que sale en el sentido de la marcha se moverá, vista desde el andén, a 600 m/s? Entonces la otra bala se moverá a 0 m/s, parecerá estar detenida.
Sin embargo, esa bala «estática» impacta en la diana ¿es la diana la que se acerca a 300 m/s a la bala?
El siguiente razonamiento es como la paradoja de Aquiles y la tortuga:
La bala en sentido contrario a la marcha del tren se acerca a 300 m/s a la diana, y la diana se acerca a la bala a 300 m/s, por tanto la bala tardará sólo 1,5 segundos en hacer impacto.
La bala en el sentido de la marcha se acerca a la diana a 300 m/s, pero la diana se aleja a 300 m/s, por tanto la bala nunca alcanzará a la diana.
Ahora sustituyamos las balas por fotones. Pero los fotones son también ondas, y una onda es una vibración, y no podemos sumar y restar velocidad a las vibraciones.
No veo que haya paradoja alguna.
En el sistema de referencia del tren, nada cambia. Las balas llegan a la diana a la vez.
En el sistema de referencia del jefe de estacion una bala se mueve a 600 m/s y la otra esta quieta. PERO EL TREN se mueven a 300 m/s, de tal manera que una diana escapa de la bala rapida y la otra «caza» a la bala lenta.
En 3 segundos la diana que se escapa, se aleja de la bala 900 m, a los que hay que añadir los 900 m que ya tenia de ventaja. Total, 1800 metros que la bala rapida (para el jefe de estacion) recorre en 3 segundos.
La diana que caza a la bala estatica (para el jefe de estacion) tiene que recorrer 900 metros a 300 m/s, luego tarda otros 3 segundos.
Por tanto el jefe de estacion mide el mismo tiempo entre que la bala se dispara y llega al blanco que el pasajero a bordo del ave.
Lo cual no seria asi si hubieramos hecho el experimento con rayos laser. Prueba a hacerte la cuenta.
Gracias!
J
Voy a hacerlo con láseres en vez de balas. Vamos a ello.
Por comodidad supondré que la velocidad del láser es también 300 m/s, en lugar de 300.000 km/s, y que esos 300 m/s es la velocidad máxima en el universo.
La cuestión clave para mí es que la bala, antes de ser disparada, lleva la velocidad del tren. Si el tren está parado, la bala lleva una velocidad de 0 m/s. Si el tren va a 300 m/s, la bala lleva una velocidad de 300 m/s.
Al ser disparada, la bala suma la velocidad que llevaba por el hecho de estar en el tren a su velocidad propia de 300 m/s. Si es disparada en el mismo sentido de la marcha, con el tren viajando a 300 m/s, ambas velocidades son positivas y dan 600 m/s. Pero si es disparada en sentido opuesto, la velocidad debida al disparo es negativa y la resultante es 0 m/s.
En cambio un láser ¿LLEVA LA VELOCIDAD DEL TREN AL SER DISPARADO?. El rayo láser no existe antes de ser disparado. Se genera, se crea en el momento del disparo. Lo mismo cualquier onda electromagnética, sea luz, radio, infrarroja …
Si decimos que el láser lleva la velocidad del tren, entonces para el láser en el sentido de la marcha se sumarían las velocidades y tendríamos una velocidad de 600 m/s. Pero hemos dicho que hay una velocidad máxima de 300 m/s, luego es imposible que se sumen las velocidades.
Si decimos que no lleva la velocidad del tren, no se sumarían las velocidades y tendríamos una velocidad de 300 m/s en ambos sentido de disparo.
Pero entonces es la paradoja: un láser nunca alcanza a la diana, el otro tarda 1,5 s. Eso es lo que ve el jefe de estación, para quien el láser viaja a 300 m/s en ambos sentidos. Para él no hay nada extraño.
En cambio el pasajero del tren ve alejarse el rayo contrario a 600 m/s, ya que se suma la velocidad del láser y la suya que se aleja de láser. De nuevo sería imposible esa suma y esa velocidad superior a la luz. Pero además es que vería el rayo en sentido de la marcha estático, de hecho para él ese rayo nunca saldría de la pistola de rayos láser.
Por tanto, para evitar esas incongruencias, hay que suponer que el rayo dentro del tren en movimiento se comporta igual que si el tren estuviera parado. Esa suposición es para mí algo «mágico».
La suposición de que el rayo dentro del tren en movimiento se comporta igual que si el tren estuviera parado sirve para explicar que para el pasajero el rayo se mueva a 300 m/s en ambos sentidos.
Al mismo tiempo el rayo se debe mover a 300 m/s para el jefe de estación.
Como ambas cosas no son posibles a la vez, hay que suponer que el tiempo transcurre de forma distinta para ambos. Eso es de nuevo algo mágico y misterioso que no entiendo.
Se lo acabo de comentar al usuario de twitter de jotdown.
La beta está mal calculada, ya que c, la velocidad de la luz, no es 300000m/s. c=300000 km/s=3×10^8 m/s, lo cual hace que beta sea más pequeña de lo que indica el artículo, siendo beta=0,00000028.
No influye en el análisis que se hace en el artículo, ya que con más razón se puede hacer la aproximación de beta~0.
Un saludo
oops!
Gracias, por supuesto que es asi… las escopetas (y las unidades las carga el diablo)!
Gracias!