Contar antes de contar

Un jabalí, una lanza para cazarlo y un sílex para despellejarlo. La cesta de la compra semanal en el Paleolítico sería algo así. De acuerdo, habría también un puñado de moras, o de castañas; muchas o pocas, pero daba igual cuántas. Un puñado. Fueron aquellos benditos miles de años en los que no había ni historia, ni prácticamente ninguna necesidad de contar una cantidad que superara los dedos de una mano. Bastaban unas muescas en un hueso para llevar la contabilidad.

Las cosas se complican cuando ese sencillo depredador que caza y recoge como cualquier otro animal se convierte en productor. Ahora hay que contar, desde berzas hasta vacas y, por supuesto, los litros que estas últimas producen. Ya no se vive de lo que da la tierra sino de lo que uno es capaz de arrancar, ordeñar, exprimir… Llega la hora de actualizar el sistema de muescas. Griegos o egipcios se las apañaron añadiendo símbolos extras (puntitos, barritas horizontales…) a esas marcas. Imaginen las cifras de las pirámides en piedras y esclavos… Los romanos simplificaron el asunto: un palito por cada oveja; una V cuando se llega a cinco y una X para diez, que no es sino lo que forman dos V unidas por la base. Seguimos con la C de centum para cien y la M de mille para mil, aunque desconocemos los vocablos originales cuyas iniciales eran L (cincuenta) o D (quinientos).

Las cosas habrían sido mucho más sencillas si los romanos hubieran conocido el cero, pero el sistema acabó adaptándose a las crecientes necesidades de una sociedad cada vez más sedienta por contar. Durante la Edad Media era habitual hacerlo en grupos de veinte, algo que, dicen, tiene su origen en contar con los dedos de las manos y los pies. Se cree que la costumbre deriva del comercio: era más sencillo contar grandes cantidades con un sistema vigesimal que con uno decimal (solo con los dedos de las manos). Otra teoría es la que relaciona este sistema con celtas, vascos o georgianos, que siguen utilizando este método. En zonas de Zamora aún se usa un cuatro veintes para ochenta, o duos veintes para cuarenta en Cantabria.

Se cree que el sistema decimal tuvo su origen en la India entre los siglos V y VII, y que llegó a Europa a través de comerciantes árabes, intelectuales o invasores de cualquier estandarte. El español también adoptó el sistema decimal, pero el francés solo lo hizo a medias: las formas antiguas —probablemente de origen celta— como vint et dix (veinte más diez), deux vints (dos por veinte), trois vints (tres por veinte), etc., se sustituyeron por trente (treinta), quarante (cuarenta) y soixante (sesenta), pero dejaron el resto de los números como solían ser en el antiguo sistema hasta hoy. No hay una explicación lógica de por qué los franceses solo transformaron una parte de sus números al sistema decimal, pero es así. 

Sea en decenas o veintenas, contar era una necesidad vital para cualquier campesino, artesano o comerciante, pero no así leer. O lo que es lo mismo: uno puede conocer las matemáticas aun siendo analfabeto. Joseph Mazur, un matemático americano, dice que la escritura aritmética precede en más de mil años a la alfabética. Paradójicamente, aprender sistemas numéricos distintos a los dominantes (arábigo y romano) es todo un desafío. Piensen que, en Europa, el georgiano o el griego son dos ejemplos de un puñado de sistemas distintos a los dominantes que se pueden contar con los dedos de una mano.

¿Por qué hablamos tan pocos idiomas numéricos en comparación con los alfabéticos? Si el sánscrito y el latín son las fuentes de las que beben los sistemas numéricos arábigo (también llamado indoarábigo) y romano, ¿podemos asumir que cada lengua tuvo alguna vez sus propios símbolos para escribir números? Nadie lo sabe. Los chinos han adoptado el sistema numeral arábigo extendido por todo el mundo, pero armonizando su uso con el de sus propios glifos, que comparten con japoneses o coreanos. También es de base decimal. África es rica en numerales autóctonos como los del antiguo etíope y, ya en América, el ejemplo más conocido de escritura matemática es el los aztecas. Era un sistema vigesimal en el que los números del uno al diecinueve se representaban con puntos y rayas, y el veinte con una bandera que se repetía para representar cantidades mayores. Y, a diferencia de los romanos, conocían el cero.

En Europa ya hemos mencionado el griego o el georgiano, pero también podríamos buscar en el ogham, que es como se llamaba el antiguo alfabeto de los irlandeses. Se conservan hasta cuatrocientas inscripciones en piedra de este tipo de escritura que se ejecutaba de arriba abajo. La inmensa mayoría de ellas recogen nombres de individuos, pero no números. No hay por qué pensar que los celtas insulares no contaran sus cosas en su propio sistema, aunque tampoco se puede descartar que conocieran ya el alfabeto latino cuando inventaron el suyo. Sin ir más lejos, los vikingos se inspiraron en los números romanos a la hora de grabar sus runas.

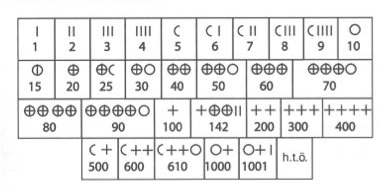
Nos quedaremos con el muchísimo menos conocido caso de los gagaúzos, una minoría de habla turca y religión cristiana ortodoxa cuyos aproximadamente 150 000 miembros viven principalmente en el sur de Moldavia. Hasta mediados del siglo XX la suya era una lengua perseguida que, como tal, apenas se escribía. Los terremotos de la geopolítica los llevaron a declarar la independencia de Moldavia en 1991, pero casi no tenían territorio físico sobre el que plantar su bandera. Durante el impasse, pasaron del alfabeto cirílico al latino que usan a día de hoy. Su sistema numeral es el arábigo, pero parece que no siempre fue así. Hace cien años, un lingüista búlgaro recuperó el código que este desconocido pueblo usaba para contar. En la magnífica ilustración de este artículo pueden encontrar sus cuatro formas básicas (barra vertical, cruz, semicírculo y círculo). El símbolo para el cien representa el valor más alto de un solo icono, lo cual puede sugerir una base decimal aunque el código se acabe articulando en base vigesimal. Se lee de izquierda a derecha y se forma de tres maneras: sumando, multiplicando por símbolos adyacentes, o por la combinación de ambas. Por ejemplo, la suma se aplica hasta cuatrocientos noventa y nueve, la multiplicación para quinientos y mil y la combinación a partir de seiscientos.

Los gagaúzos, que ya hemos dicho antes que son muy pocos, están perdiendo su lengua frente a las dominantes en la zona y probablemente ya no quede ninguno que sepa escribir los números como sus antepasados. Lingüistas como Karl Menninger clasifican la escritura matemática gagaúza como «numerales para campesinos»; símbolos que una persona analfabeta puede identificar y reproducir fácilmente. En su extremada sencillez recuerdan a los glifos que los tuareg llevan grabando en la arena del desierto desde hace más de dos mil años para contar camellos, dunas o estrellas. Irradian esa belleza primigenia y atemporal; hay algo atávico en ellos que nos reconecta con los tiempos en los que todo estaba aún por contar.