Este artículo ha sido finalista del Concurso de divulgación Ciencia Jot Down en la modalidad de ensayo. caos
Todo comenzó en una oficina del quinto piso del Edificio 24 del Instituto Tecnológico de Massachusetts (MIT, por sus siglas en inglés). Es 1963 y un meteorólogo llamado Edward Lorenz se encontraba estudiando los sistemas convectivos atmosféricos. La tarea no era sencilla, ya que las ecuaciones que gobiernan estos fenómenos resultaban complejas de manipular; obtener soluciones analíticas a las ecuaciones estaba fuera de toda discusión. Sin embargo, Lorenz se las ingenió para simplificar las ecuaciones a tan solo un conjunto de tres ecuaciones diferenciales ordinarias que describían la intensidad del movimiento convectivo, la diferencia de temperatura entre las corrientes ascendentes y descendentes, y la distorsión del perfil de temperatura vertical (es decir, qué tanto se desvía de la linealidad).
En general, podemos considerar a las ecuaciones diferenciales como «máquinas matemáticas del tiempo»: nos permiten conocer la evolución de un fenómeno —el clima, en este caso— hacia adelante y atrás en el tiempo. Para «echar a andar» estas «máquinas del tiempo» se requiere conocer las condiciones iniciales(en qué punto del espacio coordenado se desea iniciar los cálculos) y los valores de los parámetros (constantes que no varían en el tiempo). El MIT había dedicado toda una oficina a la computadora Royal McBee LGP-30, principalmente por el ruido que emitía al realizar los cálculos numéricos. Con ayuda de miss Ellen Fetter en la programación de las ecuaciones diferenciales, Lorenz ingresó ciertas condiciones iniciales a la computadora.

En algún punto de aquel día, Lorenz detuvo los cálculos y los repitió, pero en esta ocasión ingresó como condiciones iniciales algunos números ligeramente redondeados, y echó a andar nuevamente la LGP-30. Después de ir por una taza de café para matar el tiempo, Lorenz inspeccionó las soluciones y notó que estas divergían paulatinamente conforme avanzaban en el tiempo (aproximadamente dos meses de clima en la simulación). Parecía como si las series de tiempo hubieran surgido de condiciones iniciales completamente distintas, y no las milimétricamente perturbadas.
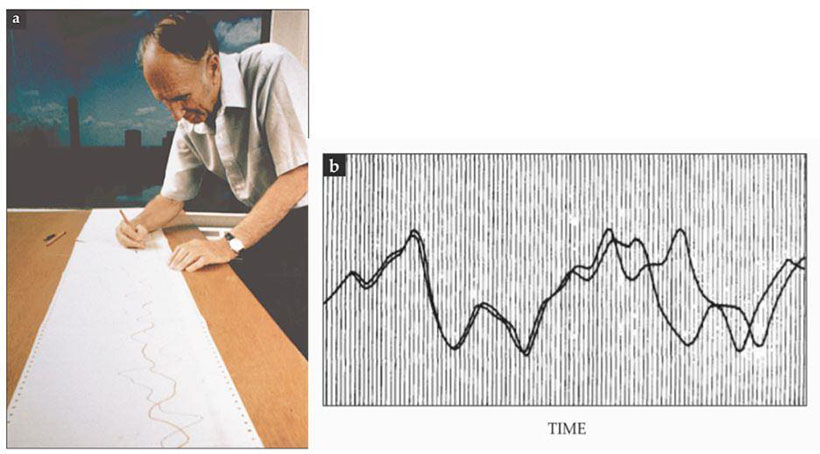
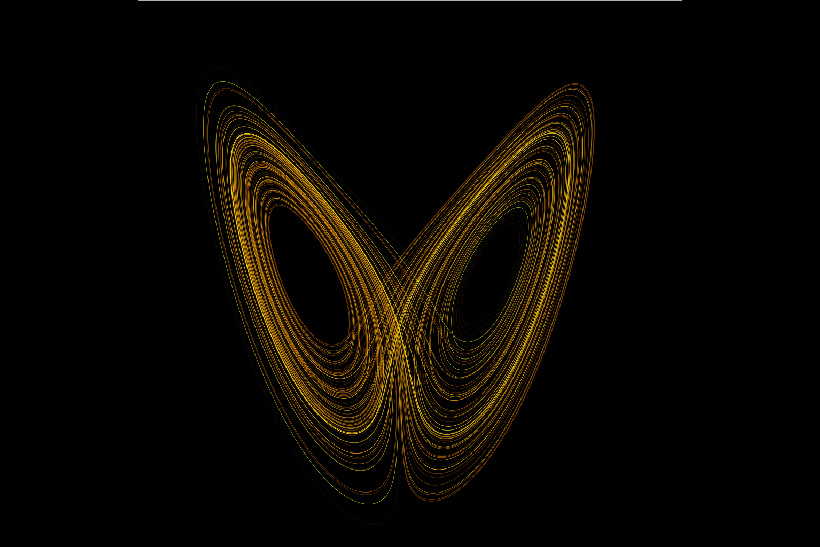
Ante esta discrepancia en las predicciones de las ecuaciones, Lorenz pensó que se trataba de errores de redondeo que se habían amplificado. Luego de descartar esta posibilidad, la explicación a la que llegó es que dicha sensibilidad extrema a las condiciones iniciales era una propiedad inherente del sistema dinámico. Más aún, las soluciones mostraban oscilaciones, pero no parecían repetirse de manera periódica, se comportaban de manera caótica, aperiódica. Espoleado por la curiosidad, Lorenz decidió prescindir del tiempo, y graficó en esta ocasión únicamente las soluciones numéricas de las tres variables que formaban las ecuaciones diferenciales: con un poco de imaginación, el patrón formado por las proyecciones asemejaba las alas de una mariposa. Se trataba de la primera visualización de un atractor caótico proveniente de un sistema dinámico.
La publicación de estos resultados no se hizo esperar1: Lorenz había encontrado el caos subyacente, e invisible hasta ese momento, del clima. La mariposa de Lorenz adquirió tonos poéticos cuando él mismo llegó a afirmar en una conferencia que «el aleteo de una mariposa en Brasil puede producir un tornado en Texas», afianzando en las mentes de nuevas generaciones de científicos una imagen que cristalizaba la incertidumbre y la belleza de las reglas que gobiernan a algunos sistemas dinámicos.
Otra de las cosas interesantes del sistema caótico de Lorenz es que cuenta con tres puntos de equilibrio que son (localmente) inestables para los valores de parámetros en los que se observa el caos. Esto implica que las soluciones de las ecuaciones diferenciales no van a converger a esos puntos; es decir, las soluciones serán repelidas por esos puntos2. Para efectos prácticos, dichos puntos de equilibrio son invisibles, y solo notaremos su existencia de manera indirecta. Para darnos una idea de esto, imaginemos por un momento que vamos «montados» como en una montaña rusa en las soluciones del sistema caótico de Lorenz. Cuando pasemos cerca de uno de estos puntos inestables, sentiremos una fuerza de repulsión que nos obligará a movernos en otra dirección: no podremos observar qué causa o de dónde proviene esta fuerza invisible, solo sentiremos su efecto sobre nosotros. Sin embargo, rodeados por estos puntos inestables, no seremos repelidos al infinito tampoco, sino que quedaremos atrapados en una región del espacio tridimensional trazando una y otra vez las alas de la mariposa de Lorenz.
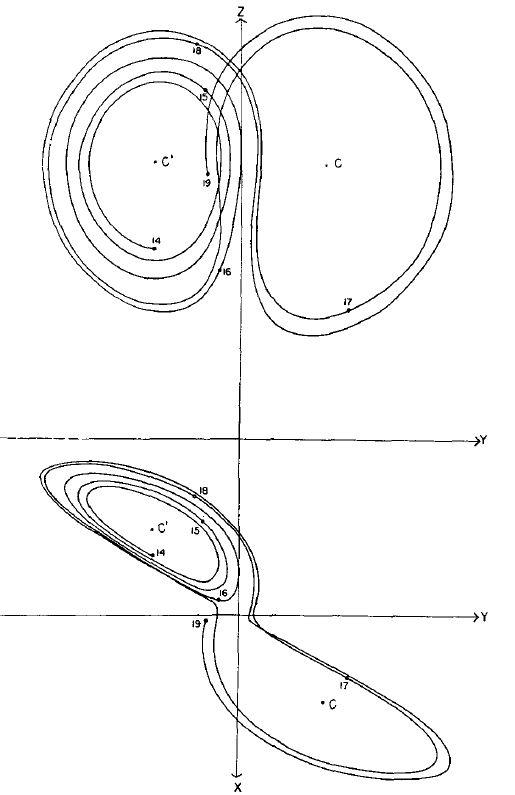
Es innegable que el descubrimiento del atractor caótico de Lorenz constituye un hito en la historia de la ciencia: abrió una ventana hasta entonces invisible para observar desde otra perspectiva el mundo dinámico que nos rodea. Desde entonces, se han diseñado y reportado todo un «zoológico» de atractores extraños provenientes de distintas ramas de la ciencia: química, física, mecánica de fluidos, etc. Entre ellos, quizá el que más destaca por la simplicidad de las ecuaciones es el sistema caótico diseñado por Otto Rössler2. Otra ventaja para su estudio es que solo cuenta con un único punto de equilibrio, el cual es inestable. A pesar de ello, nuevamente, las soluciones no se ven repelidas hacia el infinito, sino que terminan confinadas en una región del espacio que asemeja una caracola.
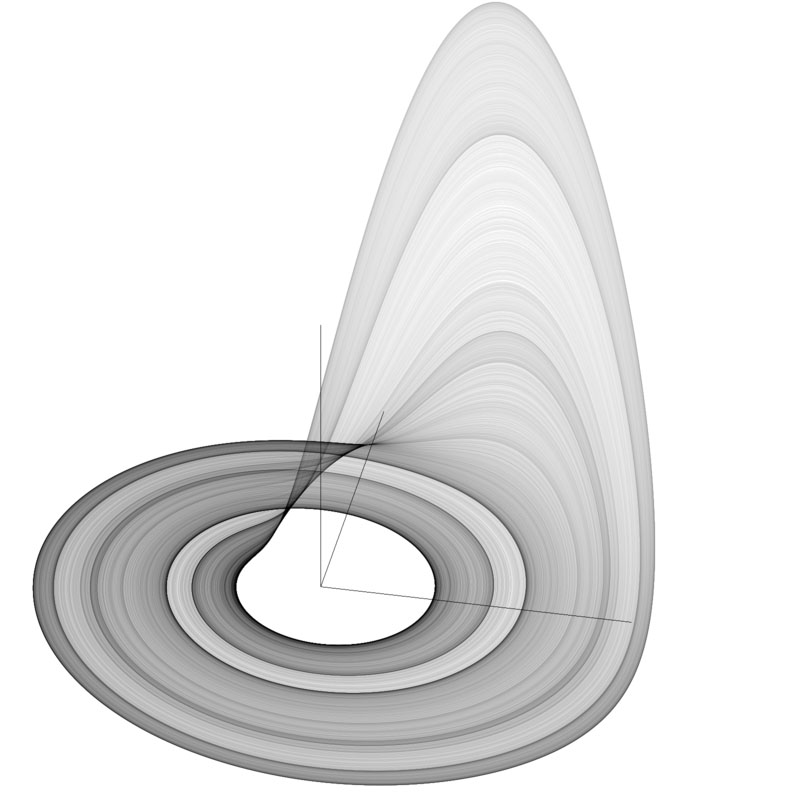
Hasta aquí podríamos decir que una semejanza entre los sistemas caóticos es la existencia de uno o más puntos de equilibrio inestables que, al cumplir ciertos requisitos matemáticos, pueden llegar a confinar a las soluciones de las ecuaciones en un espacio que forme un atractor caótico extraño semejante o más elaborado que el de Lorenz o Rössler. Esto habría de acabar medio siglo después del descubrimiento de Lorenz.
Corre el año 2012 y un par de científicos —Xion Wang y Guanrong Chen— publican en ocho páginas un nuevo hito en el campo de los sistemas caóticos3: un sistema de tres ecuaciones diferenciales ordinarias con un único punto de equilibrio estable, pero capaz de exhibir un atractor caótico.
¿Cómo es esto posible? En principio, al existir un único punto de equilibrio estable, todas las soluciones del sistema deberían converger a él; en otras palabras, se esperaría una dinámica insulsa. Pero esto no es lo que sucede.
Imaginemos por un momento un tazón en el cual soltamos desde distintos puntos de su borde varias canicas (es decir, las soluciones de las ecuaciones diferenciales). No tendremos problema en imaginar —y la experiencia nos lo dicta también— que todas las canicas, sin importar dónde las soltemos, eventualmente alcanzarán el fondo del tazón. Pero ¿cómo pensaría usted si, al soltar las canicas, algunas llegaran al fondo, y otras quedaran atrapadas, frenéticamente danzando en una región sin nunca tocar el fondo del tazón?
¿Contraintuitivo? Sí. ¿Imposible? No. El sistema caótico desarrollado por Wang y Chen constituyó un cambio de paradigma en lo concerniente al campo de los sistemas dinámicos caóticos: es posible la existencia de sistemas con un único punto de equilibrio estable, pero con una región invisible donde las soluciones se comportan de manera errática, caótica. Esta nueva clase de atractores invisibles en primera instancia fueron bautizados como atractores escondidos u ocultos (hidden attractors). En estos sistemas la estabilidad coexiste con el caos, el cual parece agazaparse como un cazador paciente y camuflado a la espera de atrapar y zarandear todo aquello que deambule en su vecindad.

También se puede pensar que esta clase atractores ocultos son raros, que se pierden en las profundidades de las colas de distribución gaussiana de lo que consideramos normal. Nada más alejado de la realidad. Desde el 2012, los científicos se han encargado de ampliar nuestro espectro visible en el campo de los atractores caóticos ocultos. Y también de trasladar estos sistemas caóticos del mundo de las aproximaciones numéricas en el computador al mundo de los circuitos integrados para volverlos más o menos tangibles, como si le otorgaran una peculiar ciudadanía para habitar nuestra propia realidad4.
Si bien la implementación de sistemas caóticos en circuitos integrados es una práctica aceptada en las revistas especializadas para considerar como «real» los sistemas caóticos, a mi parecer siguen siendo una representación a medio camino entre el mundo teórico, etéreo de las computadoras, y aquel que experimentamos de manera cotidiana. No estoy diciendo que los sistemas caóticos no existan; de hecho, la existencia del atractor caótico de Lorenz se ha demostrado rigurosa y matemáticamente: el caos no es una mera ilusión numérica5.
Así, pues, al conocer la existencia de los atractores caóticos ocultos, me vino a la mente una pregunta de naturaleza alquímica: ¿Será posible construir un sistema dinámico caótico con un atractor oculto cuyas ecuaciones provengan o describan una red de reacciones químicas? De ser así, ¿cómo lucirían estas redes de reacción química? ¿Qué ventaja(s) o desventaja(s) ofrecería a un organismo vivo contar con reacciones bioquímicas que puedan exhibir un atractor caótico oculto?
En general, averiguar el mecanismo químico a partir de la dinámica observada es una labor ardua, que requiere de mucha experiencia e intuición tanto química como matemática; en otras palabras, se trata de una labor artesanal.
Sin embargo, pensé, podríamos usamos las ecuaciones de Wang y Chen como plantillas para generar las ecuaciones diferenciales que provengan de un mecanismo de reacción. Y aquí es pertinente una observación técnica: no todas las ecuaciones diferenciales pueden interpretarse como provenientes de un mecanismo de reacción química. Afortunadamente, otros científicos han hallado la manera de transformar casi cualquier sistema caótico a mecanismos de reacción química a través de factorizaciones y escalamientos apropiados de las variables6.
Siguiendo estas metodologías, obtuve dos mecanismos de reacción que, al resolver numéricamente las ecuaciones diferenciales que emanan de estas reacciones químicas, replican la existencia de un atractor caótico oculto como el reportado por Wang y Chen7.
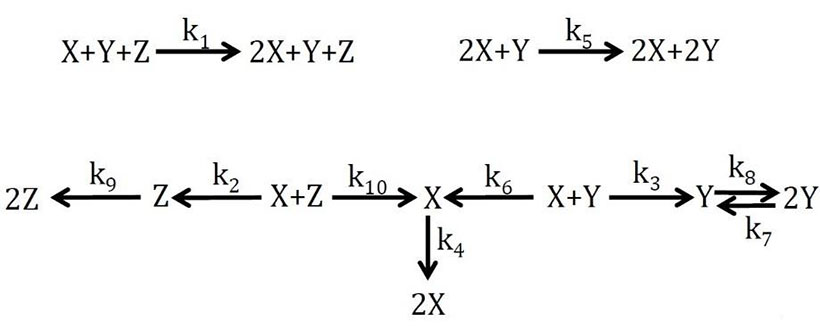
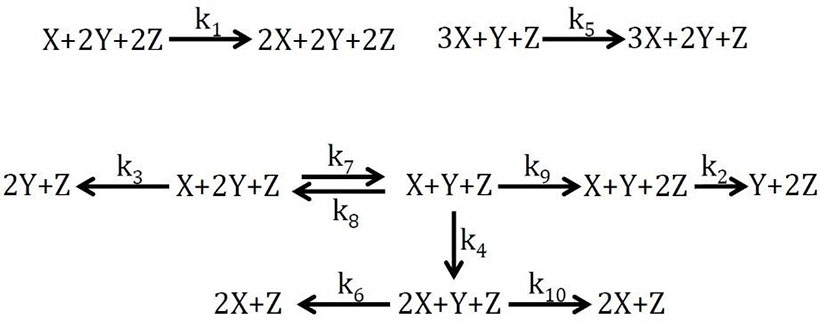
¿Tienen sentido químico estos mecanismos de reacción? ¿Son plausibles? ¿Pueden llegar a existir en la naturaleza? Tal y como están escritas las reacciones, lo dudo, aunque ningún análisis exhaustivo se ha realizado hasta el momento. El principal inconveniente de las representaciones químicas del sistema de Wang y Chen reside en la necesidad de contar con tres o más moléculas en algunas reacciones: la probabilidad de que tal cantidad de moléculas choquen entre sí, y en la orientación adecuada para que tenga lugar la reacción, es muy baja.
Sin embargo, aún existe un atisbo de esperanza para diseñar reacciones que empleen un menor número de moléculas. Por ejemplo, para darnos una idea del tamaño del universo de representaciones químicas de los sistemas caóticos por explorar, en el 2015 se reportaron más de cinco mil mecanismos químicos del sistema caótico de Lorenz6. ¿Cuántos existirán para el sistema del atractor caótico oculto de Wang y Chen? ¿Existirá una representación que no ocupe más de tres moléculas en sus reacciones? No se sabe a ciencia cierta, es una pregunta abierta hasta el momento. Inclusive, contar con una demostración matemática de por qué no podrían obtenerse un sistema químico con esas características también arrojaría luz sobre muchos otros fenómenos dinámicos. Los resultados negativos también abren yacimientos de conocimiento.
A pesar de que los dados parecen estar cargados hacia lo imposible, la idea de explorar los límites de las representaciones químicas del sistema de Wang y Chen de vez en cuando me escoce la curiosidad. Por ello busqué alternativas de colaboración para sintetizar las reacciones químicas caóticas. Así, en 2018 contacté en los Estados Unidos al doctor David Soloveichik, quien ha logrado avances en el campo de la programación de redes de reacción química usando como sustrato el ácido desoxirribonucleico (ADN). Tras compartirle las redes de reacción, le pregunté si tales sistemas eran sintetizables usando su metodología. La respuesta no fue un «no» rotundo 8. A pesar de la complejidad de las reacciones, en principio podrían llevarse a cabo, aunque a nivel experimental se enfrentaría con retos técnicos no resueltos del todo… de momento. La posibilidad de materializar un paradigma sigue latente.
Si hay algo que nos distingue como especie es que somos constructores, para bien o para mal, de lo inesperado, de lo que se considera imposible. En lo que me resta de vida, quizá no llegue a ver cristalizada experimentalmente alguna representación química del atractor caótico oculto de Wang y Chen. Y si lo llego a ver, será como espectador y no como presentador en este circo de sorpresas que es la ciencia, sentado en mi butaca mientras se escuchan los redobles de tambores y alguien más recorre la cortina para el acto que llenará las tres pistas —el pasado, presente y futuro— de una química que nos abrirá los ojos a otras maravillas: una química de lo invisible.
Notas
(1) E. N. Lorenz, «Deterministic nonperiodic flow,» Journal of the Atmospheric Sciences, vol. 20, pp. 130-141, 1963.
(2) S. Strogatz, Nonlinear dynamics and chaos: With Applications to Physics, Biology, Chemistry, and Engineering., CRC Press, 2019.
(3) G. C. Xiong Wang, «A chaotic system with only one stable equilibrium,» Communications in Nonlinear Science and Numerical Simulation, vol. 13, nº 3, pp. 1264-1272, 2012.
(4) N. V. K. G. C. Xiong Wang, Chaotic Systems with Multistability and Hidden Attractors, Springer Verlag, 2021.
(5) I. Stewart, «The Lorenz attractor exists,» Nature, vol. 406, pp. 948-949, 2000.
(6) Z. A. Tuza, Structural Analysis of Kinetic Systems with Application to Cell-free Expression Systems. Tesis Doctoral. Universidad Católica de Pázmány Péter, 2015.
(7) J. M. Méndez, «Theoretical chemical representations of a chaotic system with a unique stable equilibrium point,» de 7th International Conference on Nonlinear Science and Complexity, San Luis Potosí, Mexico., 2018.
(8) D. Soloveichik, Comunicación personal. 11 julio 2018.
(9) D. K. C. Adilson E. Motter, «Chaos at Fifty,» Physics Today, vol. 66, nº 5, pp. 27-33, 2013.
(10) Wikipedia, «Atractor de Rössler,» 11 febrero 2021. (En línea). Disponible en: https://es.wikipedia.org/wiki/Atractor_de_R%C3%B6ssler. (Último acceso: 12 mayo 2022).











