¿Quién encargó esto? (II): Ceci n’est pas une toupie

(Viene de la primera parte)

A estas alturas del siglo XXI, cabría esperar que el muón, ya todo un octogenario, se tomara la vida con más calma. Pero un camorrista nunca ceja en buscar bronca, por más años que pasen y el muón, el más pendenciero de los leptones, vuelve a estar de moda entre los físicos de partículas y los periodistas. Los resultados recientes de dos experimentos, uno en Fermilab y el otro en el CERN, arrojan resultados que no acaban de cuadrar con el canon. En la entrega anterior contábamos la infancia del muón y explicábamos el primer misterio —aún no resuelto— que desveló su descubrimiento, a saber, la extraña decisión de la naturaleza de producir tres copias de sí misma. En esta segunda parte, proponemos al lector un paseo virtual por el laboratorio norteamericano de Fermilab, donde se está llevando a cabo el experimento g-2, cuyos resultados recientes han causado no poco revuelo. Los titulares, como no puede ser menos en los tiempos que vivimos, auguran un descubrimiento que podría sacudir los cimientos de la física. Y, de hecho, podría ser así. Pero como casi todo en el mundo real —un mundo al que las redes sociales son cada día más ajenas—el posible descubrimiento hay que tomárselo cum grano salis. 

Para empezar: ¿qué es el experimento g-2?

Imagine el lector una peonza lanzada diestramente, en la época en que los niños sabían bailar peonzas. La palabra bailar venía a cuento, porque la peonza no solo se desplazaba por el piso mientras giraba a toda prisa, sino que su eje de rotación bailaba —la palabra correcta sería precedía— mientras lo hacía. De hecho, esa precesión se volvía más y más fuerte a medida que le peonza perdía velocidad, hasta que al fin se perdía el equilibrio y el juguete rodaba por los suelos. 

Una peonza que gira tiene asociada una propiedad física llamada momento angular, que describe ese giro y que no es sino el producto de la masa del objeto por su velocidad de giro. Por ejemplo, una peonza de cierta masa que gira a cierta velocidad, tiene el mismo momento angular que otra del doble de masa que gira a la mitad de velocidad, o bien que una tercera con la mitad de masa que gira al doble de velocidad. Si imaginamos al muón como una peonza, podemos asociarle por lo tanto un momento angular, o espín, palabra derivada del inglés «spin» que  significa «giro». 

El cuadro superior de la figura 1 muestra una peonza bailando en el piso, dando vueltas en torno a un imaginario círculo gracias al impulso que le ha proporcionado el diestro lanzamiento de nuestro alter ego infantil. O quizás no. El cuadro de al lado es un célebre retrato de Magritte donde se enuncia Ceci n’est pas une pipe.  El dibujo de una pipa, nos recuerda el artista, no es una pipa, sino una representación, más o menos aproximada, del objeto físico. Y de hecho, los trazos del lienzo componen un objeto plano —la sensación de volumen es un truco visual— que evoca en nuestra mente una pipa que no existe. Pues bien, un muón no es una diminuta peonza, ni siquiera una minúscula esfera girando sobre sí misma. El objeto físico, si admitiera una descripción clásica, sería más bien un punto y un punto no puede girar. Pero lo cierto es que la metáfora del punto tampoco es válida. Del muón, como de todas la partículas elementales, solo sabemos lo que el lenguaje de las matemáticas y los resultados de nuestros experimentos nos permiten entrever. Y en términos matemáticos, el muón posee una propiedad llamada espín que podemos imaginarnos como el momento angular asociado a la peonza que no es.   

El espín del muón no es solo un concepto matemático. Desde hace muchos años, los físicos de partículas sabemos medirlo. Para ello, se «prepara» un haz de muones por el expeditivo procedimiento de estrellar un haz de protones contra un blanco hecho, por ejemplo, de grafito (figura 2). En esas colisiones, que pulverizan los átomos de carbono del blanco, se producen innumerables piones (una metáfora inexacta pero muy gráfica sería imaginarnos los piones como las chispas que saltan cuando el pesado martillo del haz de protones golpea el yunque del blanco). Los piones, a su vez, se desintegran en muones. Las leyes cuánticas de esta desintegración dictan que el espín (o eje de giro) del muón apunta en la dirección contraria a su movimiento (o, en la metáfora de las peonzas, todos los muones girarían en el mismo sentido y serían, además, levógiros). La culpa de este curioso comportamiento (lo normal sería esperar que aproximadamente la mitad de los muones fueran levógiros y la otra mitad fueran dextrógiros) la tienen los neutrinos, pero esa es otra historia. Dicho sea de paso, en las colisiones protón-núcleo, los piones negativos son rápidamente absorbidos por la materia y solo escapan los positivos, que a su vez se desintegran en muones de carga positiva… que resultan ser partículas de antimateria. Se trata de un detalle irrelevante para el experimento (desde el punto de vista físico la materia y la antimateria son equivalentes, una vez que se invierten sus cargas) pero que no deja de tener su resonancia de novela tecno-pop o cómic de Marvel. Mira tú por dónde, cualquier estudiante de doctorado en el CERN o Fermilab maneja todos los días haces muónicos de antimateria, algo que solía ser exclusividad de los laboratorios Stark.

Estos (anti) muones polarizados (esto es, girando todos al unísono) se desintegran al cabo de un par de millonésimas de microsegundo a (anti) electrones y neutrinos. Los electrones se emiten preferencialmente en la dirección del espín del muón (la culpa vuelve a ser de los neutrinos). Si ahora montamos un dispositivo experimental capaz de detectar esos electrones, la medida de su distribución angular (es decir la cantidad de muones que registramos en diferentes ángulos con respecto a la dirección de vuelo), nos permite medir la dirección del espín. 

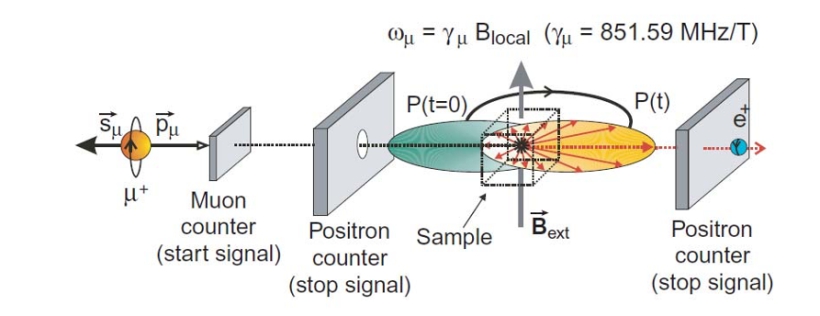
Ahora bien, si una partícula tiene carga eléctrica es posible hacerla girar en círculos aplicando un campo magnético perpendicular a su dirección de movimiento. Si además tiene espín, podemos medir un «momento magnético», que no es otra cosa que el resultado de la interacción entre el espín y el campo magnético. Una manera gráfica —y tan metafórica como las otras que hemos visto aquí— de imaginarnos el momento magnético es como una especie de masa adicional que el muón adquiere como resultado del «roce» de su espín con el «fluido magnético». En términos matemáticos:

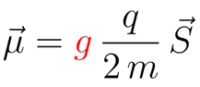
En la ecuación de arriba, μ es el momento magnético y S es el espín. Vemos que ambas cantidades son proporcionales, esto es, idénticas salvo por una constante que las multiplica, que a su vez es el producto de la carga del muón (+1 en este caso), la inversa del doble de su masa y un número «g», que en física clásica (esto es si los muones fueran esferas levógiras girando entorno a un campo magnético) valdría exactamente 1. Pero los muones no son esferas, sino objetos que siguen las leyes de la mecánica cuántica. Si utilizamos la llamada «mecánica cuántica relativista» (descrita por la bellísima ecuación de Dirac de la que hablábamos en la entrega anterior) para calcular el valor que relaciona el momento magnético y el espín, obtenemos que g =2. Este resultado es, de hecho, una revolución, un mazazo a los cimientos de la física, como han anunciado los titulares recientemente… excepto que la teoría que predice que g vale 2 en lugar de 1, dando al traste con cualquier pretensión de que las partículas elementales se comporten como objetos clásicos, se conoce desde hace casi un siglo.

De hecho, cuando medimos g en el laboratorio, obtenemos un valor muy cercano, pero no exactamente igual a 2.  Desde hace décadas, los experimentos que miden «g» haciendo girar un haz de antimuones en un anillo (ver la figura 3) y registrando los positrones que estos emiten en su desintegración son capaces de medir esta cantidad con una precisión de diez cifras significativas. En particular, el reciente resultado del experimento «g-2» de Fermilab que ha transcendido recientemente a los medios es:

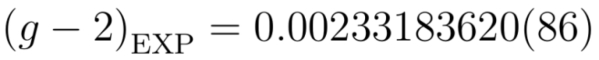
Donde el error, como puede verse, está en las últimas dos cifras decimales. La medida se expresa en términos de «g-2», es decir, sustrayendo el valor «2» a la medida de g. Como podemos ver, el momento magnético del muón no vale dos, sino un número ligeramente mayor.

Pero ese resultado, en sí mismo, no es sorprendente. De hecho, lo sorprendente sería lo contrario. La ecuación de Dirac (cuya predicción arrojaba g=2) ha sido reemplazada desde hace muchas décadas por la teoría cuántica de campos, que predice que el «vacío» —un concepto que, clásicamente quiere decir, «espacio sin nada» y que ha traído siempre de coronilla a los filósofos— es, en realidad, un hervidero de partículas elementales, las cuales, eso sí, se crean y se destruyen lo bastante rápidamente como para pasar «desapercibidas». ¿Quiere eso decir que vivimos en un universo de locos, donde es posible violar la conservación de la energía (crear un par de partículas de la nada) siempre que estas se aniquilen lo bastante rápido? Ni más ni menos. Para quitarle hierro al asunto, los físicos nos referimos a estos fantasmas cuánticos como «partículas virtuales». Pero eso sí, virtuales y todo, su presencia altera el valor del momento magnético del muón, aumentándolo en un poco más del 1 por 1000. De ahí que las primeras cifras decimales de g-2 no sean ninguna sorpresa. Son exactamente las que nos esperamos. 

¿Qué partículas virtuales interaccionan con el muón? Pues bien, todas las que la naturaleza pueda crear, lo que incluye las que conocemos y quizás algunas que no conocemos.

Esto nos lleva a una interesante posibilidad. Si somos capaces de medir con extraordinaria precisión el momento magnético del muón y somos capaces de calcular con la misma precisión las contribuciones a ese momento magnético de las partículas conocidas, entonces podemos comparar ambos valores. Si hubiera una diferencia significativa entre ellos, podríamos concluir que estamos viendo el efecto de nuevas partículas que no conocemos, o, para ser más exactos, los fantasmas de estas partículas estarían afectando, aunque fuera muy ligeramente el valor de g-2. ¿Quién dijo que los científicos no creemos en los espíritus?

Como hemos visto más arriba la medida experimental es muy precisa y no es por casualidad. El experimento de Fermilab es la continuación de otro que se desarrolló en el laboratorio de Brookhaven, diez años antes. Entre ambos, el esfuerzo de medir con diez cifras decimales g-2 ha abarcado nada menos que de dos décadas. ¿Pero qué hay de las predicciones teóricas?

Resumámoslo en un número y un gráfico: la teoría predice un valor menor que el experimento y casi incompatible con éste dentro de los márgenes de error, esto es:

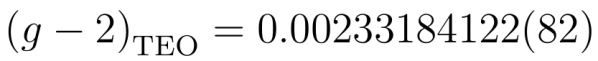
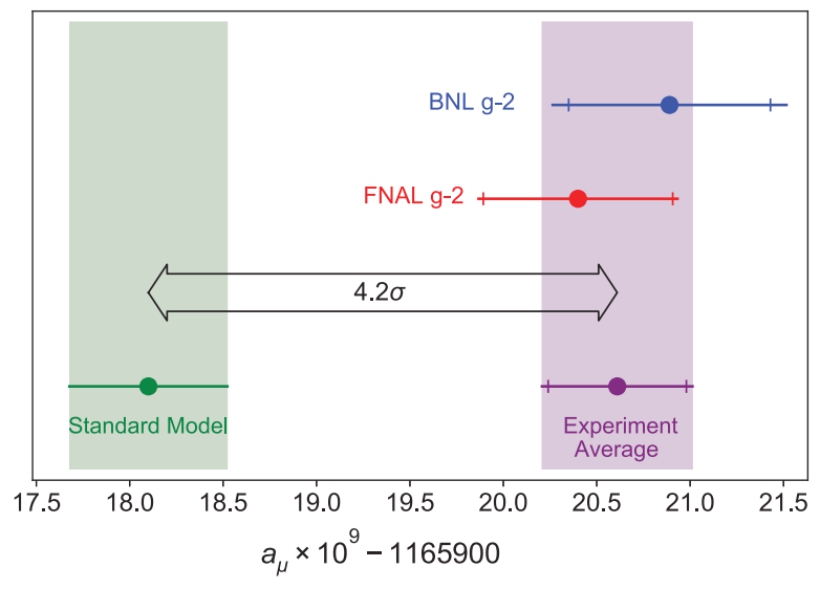
La «distancia» que separa el valor central de la predicción teórica (Modelo Estándar, en verde) y el valor experimental (promedio de los dos experimentos, el de Brookhaven y el de Fermilab) es de «4.2 sigma», esto es, 4.2 veces la barra de error de las medidas. La probabilidad de que esta discrepancia se deba a una fluctuación estadística es muy pequeña. De ahí podríamos concluir que:

EL MUÓN CUESTIONA LAS LEYES DE LA FÍSICA

NUESTRA MEJOR TEORÍA DEL UNIVERSO SE TAMBALEA 

Y otros titulares por el estilo, que, en cierto modo, producen en el lector el famoso efecto de Pedro y el lobo. La prensa es tan aficionada a echar las campanas al vuelo cada vez que hay un resultado interesante en física, el sufrido ciudadano oye tan a menudo el grito de «que viene el lobo y se come al Modelo Estándar» que, al final, nadie se toma en serio la noticia, lo que obliga a la prensa a exagerar aún más la siguiente y así ad infinitum. 

Pero… ¿hay o no hay lobo? La respuesta, como suele ser muchas veces el caso en la ciencia practicante (que no sabe nada de titulares ni de Twetter) es: «no lo sabemos todavía». 

El resultado de la figura anterior, se corresponde al promedio de cálculos teóricos realizados mediante una serie de técnicas muy sofisticadas, que, no obstante, precisan de ciertas aproximaciones (por eso el resultado se muestra con una barra de error, que nos recuerda que las predicciones no son exactas). Pues bien, existen otras técnicas que permiten realizar el mismo cálculo, evitando las aproximaciones a las que nos referimos, siempre que se disponga de suficiente capacidad de cálculo numérico. El resultado de estos cálculos se resume en la figura 5:

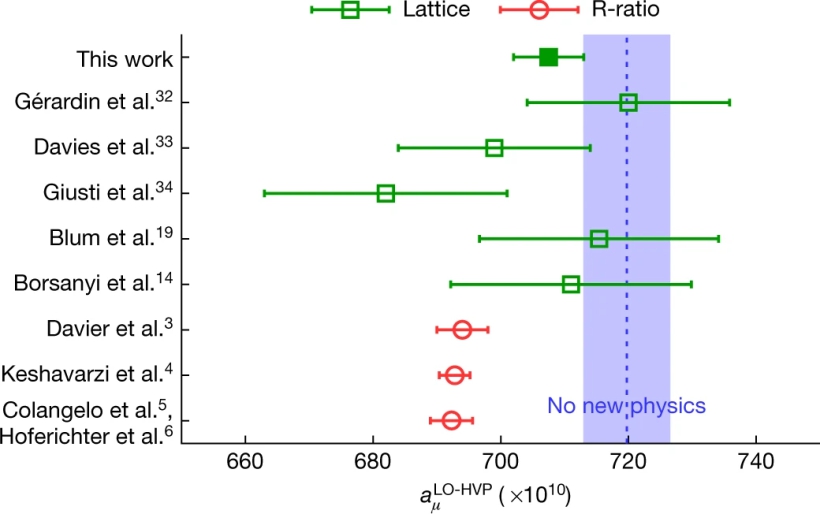
En la figura, los círculos rojos muestran diferentes cálculos utilizando la técnica «aproximada» (R-ratio) mientras que los cuadrados verdes se corresponden a la técnica más exacta pero que requiere mayor potencia de cálculo (Lattice). Reparemos que todos los resultados verdes, menos uno, tienen barras de error grandes (esto se debe precisamente a que, hasta el momento, no se había conseguido la gigantesca potencia computacional necesaria para hacer la cuenta). Pero el resultado marcado como «This work» y recientemente publicado en la prestigiosa revista Nature presenta una barra de error tan pequeña como los cálculos «clásicos». Por otra parte, este resultado está a tan solo 1 sigma del valor central del experimento y es por tanto perfectamente compatible con este. En otras palabras, si tomamos como referencia teórica el último valor de la técnica «exacta», no hay nueva física que valga, ni realidad que se tambalee, ni lobo que se coma el Modelo Estándar.  

¿Pero quién tiene razón entonces, los círculos rojos o los cuadrados verdes? Si la ciencia fuera democrática, podríamos someterlo a votación, o opinar en nuestras páginas de Facebook de acuerdo a nuestra particular fe en uno u otro modelo. Pero los resultados de los experimentos no se votan y la idiosincrasia de los científicos, aunque puede crear ruido a corto plazo, es irrelevante a la larga. 

¿Cómo se resolverá el asunto? Pues, por una parte, el excelente experimento de Fermilab continuará tomando datos y reducirá todavía un poco más su error. Por otra, auténticos ejércitos de físicos teóricos que trabajan en las teorías «opuestas» seguirán mejorando sus cálculos y tirándose entre sí de los pelos. Antes o después, unos y otros entenderán lo bastante bien su metodología como para converger a un resultado. 

¿Cuánto llevará? Unos pocos años, con suerte, pero también podría ser más tiempo. No sería la primera vez, ni la última (ahí están el ejemplo de las oscilaciones de neutrinos, el bosón de Higgs o la búsqueda de neutrinos de Majorana que todavía sigue en marcha) que un descubrimiento requiere muchas décadas. 

El resultado podría ser, que, finalmente, hayamos encontrado nueva física. Quizás nuevos leptones, (primos hermanos del electrón, el muón y el tau), o nuevas interacciones de la naturaleza, o más bosones de Higgs o materia oscura… a uno de los autores de este artículo, físico teórico de oficio, se le ponen los ojos en blanco soñando con las posibilidades. El otro, físico experimental que ya peina alguna cana, refunfuña entre dientes, repitiendo que mucho ojo con las prisas… pero en el fondo sueña, como su joven colega, con que el muón nos de otra sorpresa y una vez más, sorprendidos y maravillados, podamos preguntar: ¿pero quién encargó esto?

(Continúa aquí)