El coronavirus y la leyenda del tablero de ajedrez

Imaginen que una empresa de telefonía llama para proponerles una fantástica oferta. El precio por llamada, les explican, está fijado de la siguiente manera: por el primer minuto de conversación les cobran 0,1 céntimos; por el segundo, 0,2; por el tercero, 0,4; por el cuarto, 0,8 céntimos y así sucesivamente. Podría parecer conveniente: muchas compañías ofrecen tarifas de prepago del orden de 5 céntimos por minuto, y en el ejemplo anterior cuatro minutos de llamada han costado 1,5 céntimos. Pero conviene echar unos números antes de aceptar: no es difícil calcular que una llamada de media hora les costaría …algo más de un millón de euros.

El avispado lector habrá caído en la cuenta de que el modelo de negocio de estos truhanes no hace sino repetir la antigua historia que nos legó el enciclopedista Ibn Khallikan y cuyo enunciado es el siguiente: como premio por enseñarle a jugar al ajedrez, el rey Sheram ofreció al sabio Sissa la recompensa que éste quisiera pedirle (en otras versiones de la historia, la recompensa es ofrecida por la invención del juego). Sissa pidió un grano de trigo (otras veces es un grano de arroz) por la primera casilla, dos por la segunda, cuatro por la tercera y así sucesivamente, hasta completar los 64 trebejos. El rey accedió de inmediato, no sin ofenderse, en alguna de las variantes del cuento, por los exiguos honorarios que Sissa le solicitaba. ¡Ay! Al intentar reunir la suma acordada descubrió que no había bastante trigo en su reino para pagar al sabio.

Es fácil calcular la cantidad de trigo que Sissa pedía. Si recorremos las casillas, numerándolas del 1 al 64, en la primera obtenemos 1 grano de trigo. En la segunda, 1x 2, en la tercera, 1x2x2, en la tercera 1x2x2x2,  … y en la 64, deberíamos recibir 1x 2 x 2x … = 2⁶³ granos.

El cálculo de la cantidad total de trigo tiene su interés y puede encontrarse en muchos sitios. Por ejemplo en [1] se estima que el sabio pedía la suma de las cosechas mundiales planetarias (modernas) durante un milenio.

Muchos libros de divulgación matemática han utilizado la leyenda del tablero de ajedrez para ilustrar las propiedades de la función exponencial; entre ellas, su capacidad para desbordar nuestra intuición, mucho más afinada para las progresiones aritméticas. Los humanos entendemos fácilmente funciones que aumentan a un ritmo constante (por ejemplo una línea recta) pero una función que aumenta proporcionalmente a su valor (esto es, una exponencial) nos confunde rápidamente.

¿Qué ley matemática sigue la propagación de una pandemia como la del Covid19? Supongamos que tenemos un grupo de población N y que cada persona de este grupo transmite la enfermedad a otras dos de fuera del grupo. Si esa transmisión se realiza en un tiempo t₀, entonces hemos doblado la población infectada (y con capacidad de infectar) siguiendo exactamente la ley del tablero de ajedrez, esto es, recorremos cada «casilla» en un tiempo t₀. La progresión, por tanto, es exponencial. Pero no olvidemos que a medida que la enfermedad avanza, la población que se ha contagiado y ya no puede contagiarse de nuevo (o bien porque se han curado o bien porque han sucumbido), también aumenta. Por tanto, cuando la población es fija, llega un momento en que el número de nuevos casos deja de crecer exponencialmente y eventualmente decrece. En el caso límite, al cabo de cierto tiempo toda la población se ha infectado y la propagación del virus cesa. Por otra parte, si el virus puede saltar a otros núcleos poblacionales, como es el caso, en cada uno de ellos se reproduce el esquema de un crecimiento inicial presumiblemente exponencial.

Durante estas últimas semanas, las declaraciones oficiales definían la evolución del foco de COVID-19 en España como «en fase de contención» y aseguraban que la mayor parte de los casos eran «importados» (dando a entender que la epidemia se circunscribía a un número limitado de ciudadanos que la traían de otros países «de riesgo»). En cuanto a las medidas que se han tomado hasta el momento, destaca la timidez doméstica frente a la energía que han mostrado otros países como Corea del Sur, China o Japón.

¿Están justificadas las drásticas medidas que se han tomado allende nuestras fronteras? ¿Son efectivas o bien sólo sirven para dañar la economía y perjudicar a las personas sin que su efecto sea relevante en la propagación de la enfermedad? La pregunta no es fácil de responder. La expansión del virus depende de muchos factores, incluyendo el número de casos iniciales, la tasa de reproducción, el periodo de incubación, la capacidad de transmitir el patógeno antes de presentar síntomas etc. Todos estos factores pueden incluirse en modelos matemáticos que permiten predecir la evolución de la epidemia e incluso la potencial utilidad de las medidas de contención. Así por ejemplo, los autores de [2] encuentran que «el control de contacto y el aislamiento de infectados pueden ser suficientes para controlar un foco de COVID-19 en tres meses». En el mismo artículo avisan de que conseguir tal control puede ser muy difícil y requiere un intenso esfuerzo de las autoridades sanitarias y la cooperación del público.

Por otra parte, sin entrar en modelos matemáticos, los datos sobre el impacto del COVID-19 están disponibles en la red [3] y tienen mucho que decir sobre la evolución de la enfermedad hasta el momento.

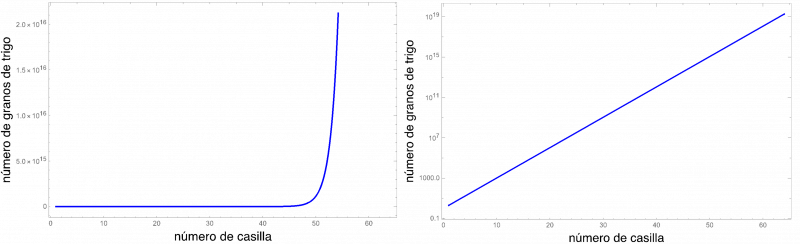
Pero antes de entrar en materia, examinemos la figura 1. El panel de la izquierda muestra la progresión del número de granos de trigo en función del número de la casilla de ajedrez. El gráfico ilustra el brutal crecimiento de la función exponencial. El panel de la derecha representa la misma función, pero utilizando una escala semilogarítmica, es decir, una escala que muestra divisiones igualmente espaciadas en el eje vertical (el que se corresponde al número de granos de trigo) marcadas con 1, 10, 100, 1000 …, en vez de 0, 1, 2, 3,… Cuando una función exponencial se representa en escala semilogarítmica los datos parecen seguir una línea recta y el ojo puede seguir mejor su evolución.

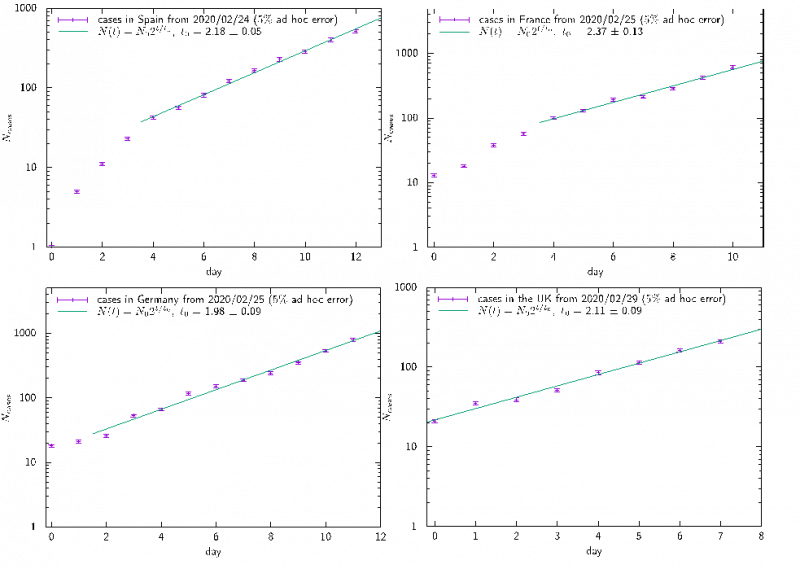
Las gráficas de las figuras 2 y 3 muestran el número de casos de COVID-19 (puntos morados) frente al número de días desde el inicio la epidemia (el día cero es el día en que empiezan a aparecer los primeros casos no aislados) en escala semilogarítmica. La figura 2 muestra los casos en España, Francia, Alemania y U.K. La línea verde que pasa con razonable precisión por los puntos azules, es un ajuste de datos al modelo N₀ 2 ^t/t0 donde t es el número de días contados desde el día cero. Esto es equivalente a  asumir que los datos se comportan como los granos de arroz y un paso en el tablero se da cuando han pasado un número t₀ de días que es el parámetro del ajuste, es decir el valor que más acerca la recta a los puntos. t₀ es por tanto el número de días necesarios para que se doblen los casos (es inmediato ver que si t₀ = 1, el número de casos se dobla cada día). Pues bien, los datos, para España, pueden describirse con una función en la que t₀ = 2.18. En la misma figura, vemos los ajustes a Francia, U.K. y Alemania. Para. Francia t₀ = 2.37, en el caso de U.K. t₀ = 2.11 y en Alemania t₀ = 1.87. Si tenemos en cuenta los errores del ajuste (es decir el error en t₀ ) concluimos que en los cuatro países, la evolución de la epidemia es similar y muy rápida, ya t₀ es del orden de 2, esto es, el número de casos se duplica aproximadamente cada dos días. Además en todos estos países, los datos pueden describirse por una sola recta en escala semilogarítmica (o sea una sola exponencial) si descontamos el crecimiento al principio del brote, que es mucho más rápido.

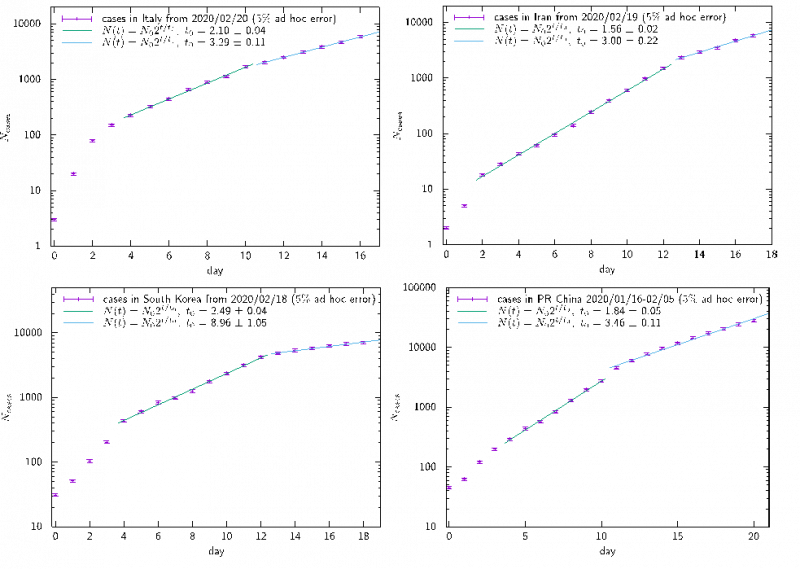
Pero hay otros países (figura 3) donde podemos apreciar dos o más exponenciales. En Italia han pasado de t₀ = 2.1 a t₀ = 3.3. En Irán de t₀ = 1.56 a t₀ = 3.0. En China, de t₀ = 1.84 a t₀ = 3.46. En Corea del Sur, de t₀ = 2.49 a t₀ = 8.96. En el caso de Japón t₀ = 7.16.

¿Qué tienen en común todos estos países? Que en todos ellos se han implementado medidas de «distanciamiento social» que van desde cerrar colegios y universidades, hasta poner en cuarentena barrios, pueblos o ciudades enteras. No nos engañemos, se trata de medidas muy difíciles de implementar, quizás más aún en países como España donde el contacto físico es parte de la cultura. Pero los modelos matemáticos como [2] sugieren que esas medidas funcionan y los datos parecen confirmarlo.

Cum grano salis, naturalmente. Los datos no nos dicen si son las medidas de contención las que están suavizando las exponenciales o si hay otros factores en juego, entre los que podría contarse el efecto de la incipiente saturación del número de infecciones. Pero la correlación es muy sugestiva.

Observe el avispado lector que el caso de España no es diferente al de los otros países. Seguir hablando de «casos importados», desde luego, es un dislate. Pero por otra parte, ¿deberíamos implementar medidas más enérgicas de inmediato, (como está haciendo Italia [4]) o conviene «ser prudentes» y no hacerlo a no ser que el número de casos aumente fuertemente?

El argumento para actuar «ya», en nuestra opinión, sería intentar evitar un posible colapso del sistema sanitario, como al que quizás estén a punto de enfrentarse en Lombardía [5]. El coordinador de la Unidad de crisis de la región de Lombardía, Antonio Pesenti, ha declarado que «el 26 de Marzo tendremos 18 mil enfermos en Lombardía, de los cuales 3,000 necesitarán asistencia respiratoria».

¿Cuántos enfermos esperamos en España el 26 de Marzo (esto es, dentro de 18 días)? Si la evolución de la epidemia sigue la ley actual y consideramos que el número inicial de enfermos es 500 (hay 516 a la hora de escribir estas líneas, el 8 de Marzo), entonces, N = 500 x 2^(18/2.2) = 145,192. Si asumimos que el diez por ciento necesitará respirador (según Pesenti el factor será más pesimista, uno en seis, en lugar de uno en 10), nos encontramos con más de 14,000 demandas en el país, o cinco veces más de lo que se considera una crisis en toda regla en Lombardía.

En cambio, si t₀ = 3.5 (como actualmente en China), N = 500 x 2^(18/3.5) = 17,665, casi diez veces menos y precisaríamos menos de 2,000 respiradores, una cantidad mucho más manejable. Y si t₀ = 9 (como actualmente en Corea del Sur), N = 2000 y el número de respiradores sería de 200. La figura cuatro compara el crecimiento de la función 2^t/t0 para t₀ = 2, t₀ = 3.5 y t₀ = 8. Las tres son exponenciales, pero implican escenarios muy diferentes.

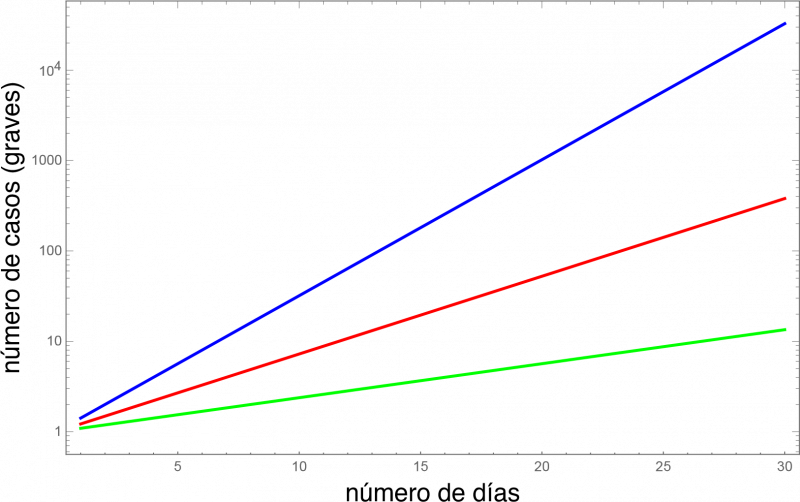
¿Va a alargarse el valor de t₀ si no se toman medidas enérgicas? Podría darse el caso, ya que hay muchos aspectos de la enfermedad que no conocemos, pero sería prudente no contar con ello. Y conviene también recordar dos datos: 1) que si el número de casos se sigue doblando cada dos días, dentro de un mes tendremos N = 500 x 2^(30/2.2) = 6.3 millones de casos y el sistema sanitario se vendría abajo con total seguridad y 2) que los datos sugieren que el tiempo que cualquier medida tarda en surtir efecto coincide (razonablemente, por otra parte) con los tiempos de incubación que parece mostrar la enfermedad: entre una y dos semanas. No parece difícil concluir que sería deseable implementar cuanto antes medidas que alarguen el tiempo de duplicación de forma sustancial. El ejemplo de Italia parece especialmente relevante.  No somos los único que opinamos así. El artículo publicado ayer en la prestigiosa revista The Lancet, bajo el título, «demasiado poco, demasiado tarde», es bastante esclarecedor:

https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(20)30522-5/fulltext?fbclid=IwAR2yBG-o09Z2fEy3f4pPaON45Qv_gpQqRslVt15dCoowMbF1wvxaSdJq1c8

En particular:

The evidence surely indicates that political leaders should be moving faster and more aggressively. As Xiaobo Yang and colleagues have shown, the mortality of critically ill patients with SARS-CoV-2 pneumonia is substantial. As they wrote recently in The Lancet Respiratory Medicine, “The severity of SARS-CoV-2 pneumonia poses great strain on critical care resources in hospitals, especially if they are not adequately staffed or resourced.” This coronavirus is not benign. It kills. The political response to the epidemic should therefore reflect the national security threat that SARS-CoV-2 represents.

Las versiones que han sobrevivido del cuento sobre la creación del ajedrez terminan de maneras muy distintas: en algunas, el inventor es recompensado por su inteligencia y se convierte en el principal consejero del rey; en otras, es castigado por exponer la ignorancia de su señor y acaba siendo ejecutado. Esperemos que la inteligencia y el buen criterio triunfen en este caso.

[1] https://matematicascercanas.com/2014/03/10/la-leyenda-del-tablero-de-ajedrez-y-los-granos-de-trigo/

[2] www.thelancet.com/action/showPdf?pii=S2214-109X%2820%2930074-7

[3] https://en.wikipedia.org/wiki/2020_coronavirus_outbreak_in_Spain y similares para otros países.

[4] https://www.lasprovincias.es/internacional/union-europea/italia-prohibira-entrada-20200307220941-nt.html

[5] https://www.corriere.it/cronache/20_marzo_07/coronavirus-stiamo-creando-terapie-intensive-anche-corridoi-cb01190a-60be-11ea-8d61-438e0a276fc4.shtml