
Este artículo ha obtenido el primer premio del concurso DIPC de divulgación del evento Ciencia Jot Down 2016
Hay afirmaciones que no solo son ciertas, sino que además son poderosas. Una de mis favoritas es, sin duda, «correlación no implica causalidad». En el mundo de los debates públicos, de las peleas en Twitter y los flames en Menéame siempre es útil contar con herramientas como esta. La frase en sí viene a significar que el hecho de que dos eventos se den habitualmente de manera consecutiva no implica que uno sea causa del otro. Así, cuando llueve es más probable que truene, pero no es la lluvia la que causa los truenos.
Imagínate que por un giro del destino te ves envuelto en una discusión sobre, por ejemplo, si el modelo de educación finés es el ejemplo a seguir en España. No tienes ni idea de pedagogía, ni del modelo educativo español, ni del finés. Si fuera una discusión en un bar no pasaría nada, podrías decir que no te interesa, pero es en internet y ya se sabe lo que eso implica. En el cibermundo no vas a reconocer que no sabes de un tema. Tienes que discutir y, aún más importante, tienes que ganar. Tu oponente dialéctico está más preparado que tú. Te bombardea con datos y estudios sobre el informe PISA, sobre los distintos métodos pedagógicos y sobre muchas otras cosas que no te interesan. Da igual, porque tú estás curtido en mil ciberbatallas y sabes como contraatacar. Esperas un momento de descuido de tu oponente. Entonces te colocas bien el palillo que sujetas con los dientes y afirmas: «Todo eso está muy bien pero no demuestra nada, porque la correlación no implica causalidad». Ni siquiera importa si estás defendiendo el modelo finés o atacándolo. Cualquier dato que se te haya dado ha quedado refutado. Correlación no implica causalidad. El debate termina y has ganado.
¿Pero tiene realmente este argumento una base sólida? No lo dudes, cualquier persona con conocimientos básicos de estadística te lo podrá confirmar. En cualquier caso vamos a indagar un poco más para que sepas usarlo correctamente. Para eso nada mejor que usar un par de ejemplos.
El ejemplo más clásico es el de los piratas y el calentamiento global. Este se basa en un estudio desarrollado nada menos que por Bobby Henderson, el creador de la Iglesia pastafari. Su intención era combatir los argumentos de los creacionistas, un grupo muy dado a encontrar correlaciones donde no las hay y a concluir que hay una causa detrás. Casualmente la causa que siempre encuentran es la misma, Dios, causa que, de nuevo casualmente, coincide con lo que estaban intentando demostrar a priori. Para ilustrar el hecho de que el que dos fenómenos se den al mismo tiempo no implica que uno cause el otro. Henderson representó la temperatura global de la Tierra en función del número de piratas en el mundo.
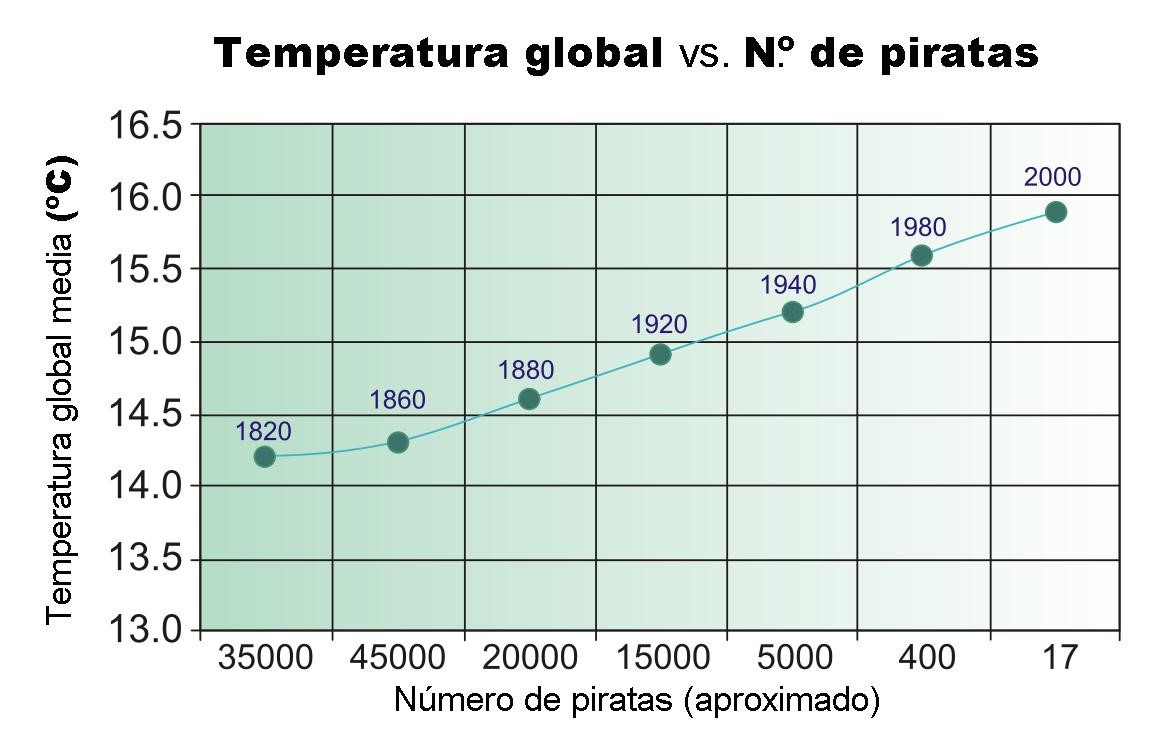
Claramente se aprecia que, a medida que el número de piratas se ha reducido, la temperatura de la atmósfera ha aumentado. Según los argumentos de los creacionistas, y otros grupos favorables a encontrar causas donde no las hay, esto significaría que la escasez de piratas es la verdadera causa del calentamiento global. No hay otra explicación. Por este motivo los seguidores de la religión de Henderson se disfrazan de piratas en el momento del culto, para combatir así el cambio climático.
Veamos otro ejemplo. La página web Spurious Correlations se dedica a buscar en distintas bases de datos correlaciones absurdas entre series de datos. Una de las más populares es la que aparece en la siguiente gráfica, que representa a través de los años tanto el número de ahogamientos en piscina producidos en los Estados Unidos como el número de películas realizadas por Nicolas Cage.
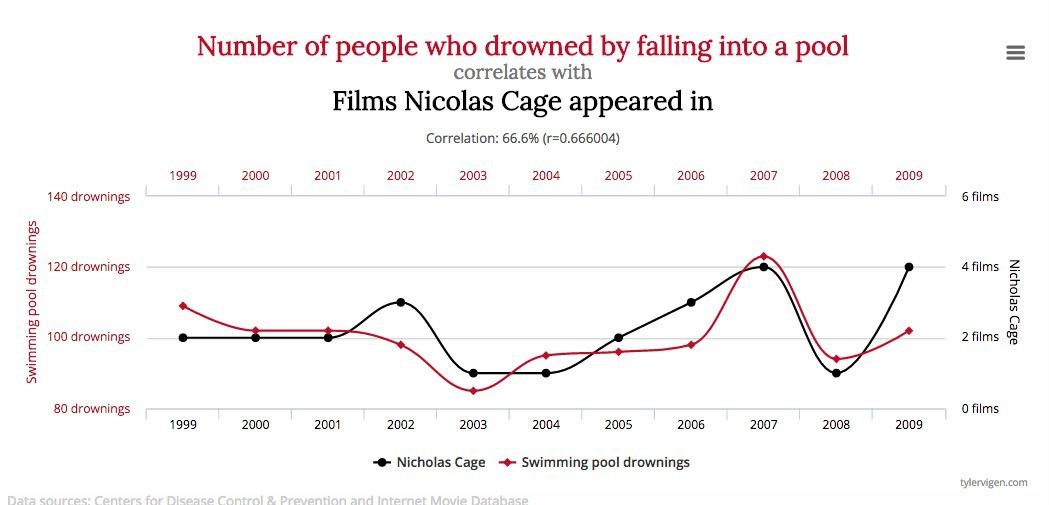
La correlación es clara. Cuantas más películas hace el bueno de Nicolas más gente muere ahogada. Lo mejor será que el pobre se retire y así ahorrará sufrimiento al mundo.
Dado que es difícil de creer que la gente se ahogue por culpa de Nicolas Cage, o que los piratas determinen la temperatura global, podemos concluir que estas correlaciones no implican que una cosa sea la causa de la otra. Veamos entonces la explicación canónica a estas gráficas. Que dos fenómenos se den a la vez, o que uno preceda al otro, no implica que uno sea la causa del otro. Aunque observamos una correlación entre A (películas de Cage) y B (ahogamientos en piscina) eso no significa que las películas de Nicolas Cage provoquen que la gente quiera morir de una manera agónica a la vez que refrescante (1).
¿Y, si no es A la causa de B, por qué se dan los dos fenómenos a la vez de forma repetida? Bueno, en general, si hay una fuerte correlación entre los fenómenos A y B, tenemos cuatro posibilidades:
- Que A cause B (que los ahogamientos en piscinas hagan que el bueno de Nicolas quiera hacer más cine para animar a las familias).
- Que B cause A (yo mismo estuve tentado de ahogarme después de ver La búsqueda 2).
- Que haya un tercer fenómeno, C, que provocara tanto A como B (es complicado imaginar alguno, pero a lo mejor el Orden Mundial conspira para reducir la población humana tanto mediante el ahogamiento como mediante el aburrimiento).
- Puro y duro azar. Hay muchos datos en el mundo, así que si los comparamos todos más tarde o más temprano encontraremos este tipo de correlaciones que no significan nada.
Este último punto es el más importante de todos, ya que no se puede demostrar que algo no ha ocurrido por azar. Así que por muchos datos que te pongan sobre la mesa tú no lo dudes. Ya tenemos una explicación sencilla y todo encaja. Las correlaciones no tienen implicación ya que todo puede ser debido a la casualidad en lugar de a la causalidad. Así que si alguien nos dice que el sistema educativo finés es el mejor porque puntúan muy alto en PISA, podemos callarlo con un firme y convencido «correlación no implica causalidad».
Ya tenemos un arma dialéctica precisa y afinada, e incluso podemos ir más allá. Si mañana nos levantamos y leemos la siguiente noticia en el periódico, no nos pasará nada.

Es evidente que ni las autoridades sanitarias ni el redactor del artículo tienen mucha idea de matemáticas. Nosotros, que estamos armados con un conocimiento todopoderoso, sabemos que no hay de qué preocuparse. La correlación no implica causalidad. Lo mismo son los yogures o lo mismo no lo son. Lo mejor será comprar esa marca aprovechando la bajada de precios. Está claro que tenemos un caso de una fuerte correlación. Todo el mundo que comió tal yogur murió. Mientras tanto, el resto de personas murieron a un ritmo normal. La correlación está fuera de duda.
Si algún alarmista viene a tocarnos las narices podemos usar el mismo argumento que antes. Tenemos correlación entre el comer yogur y el morir, así que tenemos cuatro posibilidades:
- Los yogures son los causantes de la muerte de las personas.
- La muerte de las personas es causante de que se comiera antes el yogur.
- Hay un fenómeno que es causa a la vez de las muertes y de que la gente coma yogures.
- Es una simple casualidad. La gente muere, la gente come yogures, ¿qué le vamos a hacer?
La segunda y tercera posibilidad son bastante improbables. Es difícil de creer que las muertes causen la ingesta de yogures o que exista un evento que provoque tanto el consumo de yogures como la muerte de los que los consumen. Sin embargo, demostrar que no es azar es difícil. La correlación es clara, pero nadie ha demostrado aún que los yogures estén envenenados.
A estas alturas el avispado lector (o la avispada lectora) ya habrá intuido que este artículo no es una defensa a ultranza de la frasecita de las narices. Seamos serios. Por mucho que estemos convencidos de que la correlación no implica causalidad, si mañana ocurre algo así no nos lo plantearíamos ni por un instante. Los yogures están envenenados. No hay otra posibilidad. Por supuesto que habrá que analizarlos para ver qué ha ocurrido, pero mientras tanto todos actuaremos guiados por la certeza de que algo ha pasado.
¿Y qué diferencia este caso del caso de los piratas o de las piscinas? Lo primero es el sentido común, que nos dice que es posible que unos yogures se envenenen, pero que es mucho más difícil que el noble oficio de la piratería afecte al clima. Lo segundo es la correlación en sí. Tenemos que tener en cuenta que no todas las correlaciones son iguales y que a partir de ellas podemos sacar muchas conclusiones. La correlación no es una magnitud dicotómica. No es algo que se tiene o no se tiene, es algo que puede ser muy grande o muy pequeño.
Volviendo al escabroso ejemplo de los yogures. Además de saber que hay una correlación, podemos estimar qué probabilidad hay de que ocurra algo así por casualidad. Imaginad que vemos en la noticia que un 0,1% de la población española consumió el citado yogur el día en cuestión. Eso hace unos 460.000 españoles muertos en un día. Este dato contrastaría con la mortalidad en todo el año 2014, que fue de 395.830 personas (según datos del INE). Ya, el que ocurra algo así es absolutamente improbable. De hecho, es lo que se suele denominar, estadísticamente imposible. Calcular la probabilidad de que esto ocurra requiere hacer suposiciones sobre cómo se distribuye la mortalidad entre la población, las edades de los consumidores de yogur y otros parámetros. Una estimación muy conservadora me da el resultado de que la probabilidad es menor que una entre 10^25 (2). Es más probable encontrar algo de principio activo en una disolución homeopática a que ocurra algo semejante por pura casualidad. Por eso podemos concluir que algo ha ocurrido, aunque aún no hayamos analizado los yogures.
¿Y qué ocurre entonces con las piscinas y las películas de Nicolas Cage? Pues ocurre simplemente que ahí la correlación no es tan grande. Ese es el quid de la cuestión y el mensaje que me gustaría que os quedase después de leer este artículo. Correlación no implica causalidad, es cierto, pero hay correlaciones más grandes que otras. Como ya hemos dicho, la correlación no es una magnitud binaria. No es tan simple como que exista o no exista. Hay correlaciones pequeñas como la de las películas de Cage, y hay correlaciones muy grandes como la del macabro ejemplo del yogur. En el ejemplo de las piscinas, la misma web que lo dio a conocer calcula la probabilidad de que sea azar, un 33,4%. Por supuesto ahí también hay suposiciones detrás, pero la manera de calcularlo es bastante estándar. ¿Es un 33,4% una probabilidad muy baja? Pues dependerá de para qué. Si tenemos en cuenta que los autores de la web analizan cientos de miles de cadenas de datos, lo improbable sería que no encontrasen ese tipo de correlaciones espurias. Simplemente analizando el número de cadenas estudiadas y las correlaciones encontradas se puede calcular la probabilidad de que sea puro azar o de que pueda tener una causa más relevante.
A esto precisamente se dedican algunos analistas especializados en big data. Analizan cantidades ingentes de datos y buscan correlaciones que nadie espera. Después, se dedican a analizar la probabilidad de que sea azar o no, y si no parece serlo lo analizan con más profundidad. Puede que dos eventos en apariencia desconectados tengan una relación causal demasiado difícil de apreciar a simple vista. Si encuentras este tipo de correlaciones, puedes llegar a ganar mucho dinero al ser capaz de predecir movimientos de los mercados que nadie más puede ver.
Nadie duda de que la correlación no implica causalidad. Científicos de todos los campos dedican cantidades ingentes de tiempo a repetir experimentos para distinguir correlaciones importantes de correlaciones espurias. Incluso se ha observado que muchos experimentos científicos con grandes correlaciones tienen una probabilidad alta de ser puramente casuales. Eso ocurre porque en el mundo se realizan muchos experimentos continuamente. La probabilidad de que nunca se dé una correlación espuria es realmente baja y son precisamente las correlaciones inesperadas las que más interesan a la comunidad científica. El único remedio para evitar esto es la repetición de los experimentos. Sin embargo, todo esto no quiere decir que las correlaciones no tenga relevancia, o que no sean indicativas de causalidad. Tenemos que saber distinguir entre correlaciones más y menos probables. Tenemos que analizar cada caso cuantitativamente y averiguar cuál es la probabilidad de que un evento sea aleatorio para saber si debemos indagar más o no.
Si nos molestamos en mirar los datos antes de aceptarlos o desecharlos, aumentaremos nuestro conocimiento del mundo. Si nos limitamos a desdeñar los datos que contradigan nuestras ideas preconcebidas con una frase hecha, a lo más que podemos aspirar es a ser el más listo de Menéame. Lo primero es deseable. Lo segundo no es algo que uno deba incluir en su currículum.
Notas:
(1) Antes de que se me acuse de atacar a Nicolas Cage innecesariamente y empecemos una discusión gafapasta sobre Leaving Las Vegas, me gustaría contraargumentar con solo dos palabras: Ghost Rider.
(2) Un uno y veinticinco ceros detrás, o si lo preferís 1000000000000000000000000.












Pingback: Correlación no implica causalidad
Como mi profesor de metodología en mi carrera de Ciencias Políticas nos explicaba. Es básico cumplir las 5 normas. Aunque cumplir las cinco era difícil, se bastaba en algunos casos con cumplir las tres primeras, siempre necesarias.
1. Aquello que consideramos factor causal debe preceder, anterior, siempre en el tiempo a aquello que consideramos factor efecto.
2. Entre aquello que estimamos como factor causal y aquello que estimamos como factor efecto debe existir una evidente relación empírica o una evidencia.
3. El investigador no podrá establecer un relación causal entre un supuesto, factor causal y un supuesto factor efecto si un tercer factor es causa de los dos.
4. El supuesto factor causal debe constituir condición necesaria para la constitución del supuesto factor efecto.
5. La relación causal debe ser tal que el supuesto factor causal sea suficiente para generar el supuesto factor efecto.
Un bien merecido premio. Buen artículo.
Como dice un viejisimo proverbio:
Una vez, mala suerte.
Dos veces, casualidad.
Tres veces, ES EL ENEMIGO.
Los más grandes expertos en correlaciones ridículas son probablemente los economistas académicos (especialmente los mainstream, es decir, los neoclásicos, que parecen vivir en otro universo). Por ejemplo, hay un articulo sobre la supuesta relación estadística entre lluvia y religiosidad. Los autores estudiaban las diferencias en la variabilidad de la lluvia entre 2.650 condados de Estados Unidos en 1860-90 y encontraban una correlación (elevada, según ellos) con el número total de miembros de religiones en cada condado. El artículo mereció una recensión en nadaesgratis.es, el conocido blog neoclásico de Economía. Pero más divertido aun es otro estudio que encuentra una relación inversa (aquí la correlación era sólo un poco más baja) entre el desarrollo económico en 1960-1985 y el tamaño del pene. Ni idea si este paper iba en serio o no, pero ahí está. Y quiero recalcar que ambos estudios fueron realizados por profesores universitarios.
«Es más probable encontrar algo de principio activo en una disolución homeopática a que ocurra algo semejante por pura casualidad»
Solo esta frase ya jsutificaba el premio. :D
Autor, sé honesto y dime que no disfrutaste de Contracara (Face…Off…). Nicolas Cage es un talentosísimo actor. Héroe definitivo de los 90. Sus malas películas solo lo engrandecen.
Un artículo muy bueno, entretenido y didáctico, sólo una cuestión, 460.000 españoles es un 1% de los habitantes de España, no un 0,1%.
Un saludo
Otro argumento clásico de los portadores de la verdad es «hacer las cosas como Dios manda», que sirve de argumento categórico y definitivo para cualquier cosa; «Hay que votar como dios manda» etc.
Lo peor es que hay personas que dejan de pensar en cuando oyen esto.
Así nos va.
Si bien es cierto que correlación no implica causalidad, esto ya hace tiempo que es bien sabido entre los investigadores que usan métodos cuantitativos. Es comprensible la excitación del lego al darse cuenta de esta verdad no tan obvia, pero me sorprende que este artículo reciba el primer premio en un concurso de divulgación. Tal vez en futuras ediciones de este premio alguien tenga la bondad de resumir los métodos que se han venido desarrollado en el terreno de la estadística desde hace varias decadas para poder estimar relaciones causales de manera más fiable que una simple correlación entre dos variables.
Desgraciadamente no por todos, Antonio. Yo diría que a las alturas que estaos son demasiados los que no lo tienen claro. Aunque, ahora que lo pienso, no son investigadores.
Me ha gustado mucho. Puede que para muchas personas el contenido del artículo sea evidente. Pero en el contexto en el que estamos actualmente, político, económico, social, electoral…Muchos políticos, «opinadores», periodistas y otros medios de influencia, establecen causalidades donde sólo hay correlaciones. Unas veces por pura ignorancia y otras por demagogia.
Creo que este artículo debería ser de lectura recomendada en colegios e institutos.
Cuanto antes entiendan nuestros jóvenes que correlación no implica necesariamente causalidad, más difícil será engañarlos.
Buen artículo para completar con este otro:
http://www.nature.com/news/statisticians-issue-warning-over-misuse-of-p-values-1.19503
Sigo el blog del autor de esta entrada desde hace años y quiero felicitarle por las muchas entradas de auténtica ciencia que nos ha regalado.
Pero, sobre esta entrada, debo puntualizar que, en mi humilde opinión el autor no merece el premio debido a que no explica algo que pivota sobre todo lo que dice: cuantos más datos se tienen, menor es el error muestral y mayor es la probabilidad de que la correlación sí implique causalidad.
Qué dices tío.
No es una cuestión de errores. Puedes tener la hostia de valores, tener una correlación estupenda con errores minúsculos y aún así eso no te va a indicar NADA de la relación de causalidad que existe entre los dos fenómenos.
Si tienes un fenómeno A y un fenómeno B, (y supongamos que sabemos que A causa B) y tienes una correlación de 1 entre ambos y todos los valores que a ti te de la gana, es evidente que la correlación entre ambos nunca va a ser prueba de causalidad por la sencilla razón de que eso no te va a permitir distinguir si es A el que causa B o B el que causa A. Por eso correlación NO implica causalidad.
Porque los dos fenómenos no pueden causarse el uno al otro mutuamente mientras que los dos sí van a correlar.
Eres el troll más cansino que he visto nunca…
La gente con blogs de ciencia tiene una paciencia contigo inmensa.
Puedo evaluar la correlación entre número de gallinas y número de huevos. La correlación puede ser muy elevada para un tamaño muestral inmenso (recogiendo datos de muchos años).
Aún así, no sabré qué es causa de qué: la gallina del huevo, o el huevo de la gallina.
Antonio, hello. Has de estar trolleando nada más, y muy bien, pero quiero dejar aquí una cosita para los que son curiosos como yo. Cuanto más datos se tienen mejor, es verdad. Sin olvidar que depende. Por ejemplo, cuando se habla de correlación de este tipo de variables, surge un error común, que aparece justamente cuando utilizas una muestra grande (que es lo más recomendado), pues hace que datos irrelevantes tengan un grado de significancia deshonesto, es decir, se corre el riesgo de que el valor P va a ser significativo incluso si no lo es, porque tu muestra es grande.
¡Qué hermoso! Si no es un experimento no se puede inferir causalidad. Por más que tu covarianza fuese de .80 o .90, no puede hacerse. ¡Es tan hermoso!
Pingback: Ver películas de Nicolas Cage aumenta el riesgo de ahogarse en la piscina | España Red Vida Saludable
Pingback: La selección española siempre ganó con Arbeloa y nunca lo hizo con Raúl: sobre la correlación y la causalidad | Al contragolpe
Pingback: ¿La peor gráfica de la historia? – Enchufa2
Pingback: Turoperador bibliotecarioEl blog de Infobibliotecas
Me ha encantado y los ejemplos son divertidísimos!
Pingback: #8 Modelos Mentales 4: Monos infinitos, helados asesinos y una ruleta en Montecarlo - Jaime Rodríguez de Santiago
«La página web Spurious Correlations se dedica a buscar en distintas bases de datos correlaciones absurdas entre series de datos. Una de las más populares es la que aparece en la siguiente gráfica, que representa a través de los años tanto el número de ahogamientos en piscina producidos en los Estados Unidos como el número de películas realizadas por Nicolas Cage.
La correlación es clara. Cuantas más películas hace el bueno de Nicolas más gente muere ahogada. Lo mejor será que el pobre se retire y así ahorrará sufrimiento al mundo.
Dado que es difícil de creer que la gente se ahogue por culpa de Nicolas Cage, o que los piratas determinen la temperatura global, podemos concluir que estas correlaciones no implican que una cosa sea la causa de la otra. Veamos entonces la explicación canónica a estas gráficas. Que dos fenómenos se den a la vez, o que uno preceda al otro, no implica que uno sea la causa del otro. Aunque observamos una correlación entre A (películas de Cage) y B (ahogamientos en piscina) eso no significa que las películas de Nicolas Cage provoquen que la gente quiera morir de una manera agónica a la vez que refrescante.»
el artículo, en su conjunto, me pareció muy interesante basado en la idea de que la correlación no implica casualidad. El párrafo que más me ha llamado la atención es el ejemplo que se ha puesto sobre la pag web Spurious, en el que trata sobre la correlación entre los ahogamientos en piscinas en EE.UU. y las películas realizadas por Nicolas Cage. Según esto, cuantas más películas hace Cage, mas ahogamientos hay. Este ejem`plo afirma y demuestra que 2 fenómenos que se den a la vez, no implica que uno provenga del otro.
jajajja, muy buen ejemplo para establecer el concepto de correlacion
Bueno y el caso de la mariposa y el caos para cuándo.
Pingback: Ayunos: ¿moda, salud o ambos? - HEALTHYINSTITUTE
Pingback: ☕✒️En Ciencia la duda no ofende – Un polizón de la vida
Pingback: David Hume y la filosofía homeopática – Jéssica Fillol – Roja y motera