Todo puede ser convertido en música
Hace algunos años, los medios difundieron una sugestiva pieza musical llamada «el sonido de Júpiter», producida a partir de las emisiones de radio del planeta gigante, recogidas por la sonda Voyager. Era, en pocas palabras, música planetaria. Y, ¿saben qué? Suena bien. Es decir, no es una canción de los Beatles, ni tiene una melodía que pueda usted cantar en la ducha, pero se escucha con agrado, es interesante. Parece la banda sonora de alguna película de ciencia ficción:
Lo mismo se ha hecho con otros planetas y astros, aunque esta de Júpiter es una de las que más me gustan. Pero, ¿es que son capaces los astros de componer música? Obviamente, la respuesta es no. Las emisiones de Júpiter pueden ser traducidas a lenguaje musical, como también pueden ser convertidas en líneas sobre una pantalla. Casi cualquier fenómeno natural que pueda ser expresado mediante números puede ser convertido en música, siempre que esos números no sean demasiado complejos. También pueden ser convertidas, cómo no, secuencias como los decimales de pi o la de Fibonacci. Al final del artículo veremos algunos ejemplos curiosos de esto. El resultado es en ocasiones fascinante, como escuchar una música venida de ninguna parte. Pero aun así surge otra pregunta: ¿cuál es el proceso? La música parece algo tan etéreo y emocional que resulta difícil imaginar que una fría lista de números, el sordo ruido de un planeta o incluso los minúsculos pulsos eléctricos de una planta puedan producirla. Y sin embargo, pueden.
La música es matemática
A diferencia del lenguaje verbal, el lenguaje musical está sujeto a leyes numéricas rígidas. En un idioma hablado, cualquier palabra puede ser dicha con diferentes acentos o pronunciaciones, incluso puede hestar mal heskrita, sin que el mensaje se pierda por el camino. Sin embargo, esto no sucede con las notas musicales. Usted no puede «pronunciar» mal una nota musical sin que el mensaje resulte inefectivo. Para que dos notas musicales formen una melodía comprensible, o para que suenen en armonía cuando son emitidas a la vez, debe haber una relación matemática precisa entre las respectivas frecuencias de sus ondas sonoras. Esa relación matemática es cuantificable. Es como una ley.
Es más, usted comprende esa relación aunque no sea consciente de ello. Todos nosotros, excepto una persona con sordera total, tenemos la experiencia de reconocer al instante si se cumplen o no las leyes matemáticas que rigen la melodía y la armonía. Obviamente los músicos profesionales tienen más facilidad y pueden captar disonancias que otras personas no perciben, pero la verdad es que cualquiera de nosotros reconoce una desafinación severa en cuanto la oye, ya sea porque hay notas fuera de frecuencia, ya sea porque hay notas que, incluso estando en sus correctas frecuencias, no deberían sonar juntas. Es algo que aprendemos a reconocer desde que nuestra madre nos cantaba canciones en la cuna. Cierto es que la mayoría de nosotros no sabemos expresar esto en términos matemáticos. Aun así, nuestro cerebro conoce estas relaciones. Esto es lo que nos permite distinguir entre una canción y el ruido del motor de un camión de dieciocho ejes. Generalmente preferimos la canción, por eso no hay emisoras dedicadas a emitir los últimos éxitos de ruidos de camión, salvo que incluyamos en ese grupo algunas emisoras de hardcore techno. Pero bueno, aunque en sonido hay muchos gustos adquiridos, la música no deja de seguir ciertas reglas físicas.
Por eso, cuando alguien que no sea sordo dice «es que no tengo oído» o «no sé nada de música», se equivoca. Claro que sabe algo sobre música. Todo el mundo sabe algo sobre música. Por ejemplo, vea el siguiente vídeo. No importa cuán desconocedor de las cuestiones musicales se considere usted, notará de inmediato que algo no va bien. Y si es usted sordo, bueno, sepa que he pensado en usted. No captará los problemas en la armonía, pero verá unos cuantos bailecitos hilarantes que son el equivalente coreográfico de una desafinación.
En este vídeo, los músicos han empezado a interpretar una canción en la misma tonalidad… todos ellos, excepto el guitarrista. El que un solo instrumento esté tocando la misma canción en otro tono basta para que todo el conjunto suene desastrosamente mal. En particular, los gorgoritos de Pitingo, que empiezan a sugerir las purgas en las mazmorras de la KGB durante un día laborable. A usted, su cerebro le ha dicho: «las relaciones matemáticas entre las notas no son las correctas».
Pero, ¿en qué tono estamos?
Cualquier formación musical, sea una orquesta sinfónica, un pasacalles o un grupo de pop-rock (excepto el de Pitingo), necesita que sus instrumentos estén afinados en la misma tonalidad, para que cuando todos interpreten una misma nota, esta suene con la misma frecuencia. Esto parece obvio. Pero ¿cómo se ponen de acuerdo los músicos sobre la frecuencia concreta que deben asignar a una tonalidad? Podríamos pensar que cada instrumento musical viene de fábrica con la afinación correcta, pero esto no siempre es así. Es más, muchos instrumentos tienen la simpática costumbre de desafinarse con el uso (o con el desuso, o con los cambios de temperatura, o con solo mirarlo, o con pensar en él). Así que se suelen necesitar ser afinados con cierta frecuencia. Esto no se aplica a los sintetizadores electrónicos, que no se desafinan, claro, aunque tienen su propio punto débil: no se les puede derramar cerveza encima.
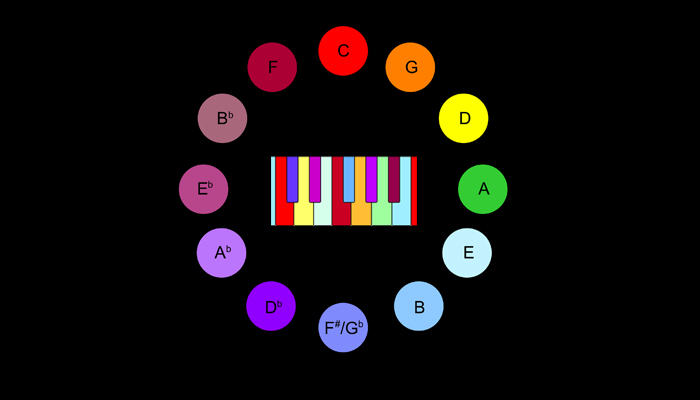
Pero incluso en el caso de que todos los instrumentos viniesen perfectamente afinados de fábrica, alguien, en alguna parte, tiene que decidir cuál es la frecuencia concreta para una afinación estandarizada. Como sonido de referencia, pues, se toma una nota concreta, llamada la4 (según la notación que se utilice, podrá verla escrita como la3, la4, A3 o A4, aunque no se preocupe, el nombre es lo de menos aquí). Escúchela aquí.
Quizá sea más fácil de entender de este otro modo: visualice el teclado de un piano. Una de las teclas blancas más cercanas al centro del teclado es el «do central». Pues bien, cinco teclas blancas a su derecha está el famoso «la4». Usted pulsa esa tecla y ese sonido se usará para calibrar la afinación de los demás instrumentos. Los músicos son capaces de, ayudándose exclusivamente del oído, afinar todos sus instrumentos en la misma frecuencia. Pero alguien tiene que dar la nota de referencia. Aquí es donde resultan útiles los diapasones y afinadores, que no se desafinan y siempre reproducen una nota con la misma frecuencia. En la actualidad existen incluso afinadores electrónicos que le dicen en una pantalla si su instrumento está afinado o no. Es más, cualquier teléfono móvil, con ayuda de una pequeña aplicación, puede servir para afinar un instrumento. Aunque en tiempos había otros métodos: una antigua botella de vidrio de cerveza Mahou, de las de un litro, solía producir un casi perfecto mi cuando era golpeada por una baqueta de batería. ¿Lo mejor? Que para obtener ese mi no servía la botella llena, así que había que vaciarla antes. Mucho mejor que cualquier cacharro electrónico.
Ahora bien, ¿quién decide la frecuencia concreta de la nota la4? Porque habrá una manera concreta en que deba sonar, pensará usted. Pues bien, no la hay. La frecuencia concreta de la4 es una convención cultural que varía según épocas y estilos musicales. Es verdad que existe una frecuencia «de fábrica» más habitual, de 440 hercios (quizá alguna vez ha escuchado usted decir que determinado instrumento está afinado «en 440», o «cuatro cuarenta»), pero esto no es una norma rígida y de hecho cualquier afinador electrónico le dará la opción de utilizar otras frecuencias de base. La elección de esta cifra depende de sus preferencias personales o de las cualidades físicas de los instrumentos que vaya a tocar. Es verdad que se fabrican muchos instrumentos pensados para sonar mejor cuando la4 está en 440 Hz pero también se producen otros que no. También hay muchos instrumentos antiguos que suenan mejor en otras frecuencias de afinación, hoy pasadas de moda.
Pero sea cual sea la frecuencia en hercios que usted elija para la4, hay algo que nunca cambia: la fórmula matemática para obtener, a partir de la4, las frecuencias de todas las demás notas musicales. Usted puede cambiar la frecuencia de la4, pero no las relaciones entre los intervalos de todas las demás notas con respecto a ella. Esos intervalos son los que determinan que la escala musical suene como suena. Por eso los trastes de una guitarra permanecen fijos en el mástil sin importar qué frecuencia elija usted para su la4. De otro modo, los trastes deberían desplazarse cada vez que las cuerdas son tensadas o destensadas, cambiando las reglas numéricas entre notas según la tonalidad. Y fabricar una guitarra funcional se volvería imposible. En un piano podría hallarse solución, pero también requeriría un ejercicio de ingeniería digno del CERN.
Piense en el típico «do, re, mi, fa, sol, la, si» que nos hacían cantar en el colegio. Son siete intervalos entre notas que corresponden a las teclas blancas del piano. Si añadimos las cinco teclas negras, obtendremos los doce intervalos posibles en una escala musical (los niños cantan solamente las teclas blancas porque cantar también las negras es muy difícil). Si en el colegio nos hicieran cantar la escala con todos los intervalos posibles, diríamos algo como «do, do sostenido, re, re sostenido, mi, fa, fa sostenido, sol, sol sostenido, la, si bemol, si». El decimotercer intervalo, el siguiente do, pertenecería a la siguiente escala, que contiene otra vez las mismas notas pero con frecuencias más altas y sonido más agudo. Estas son las doce notas con las que se compone toda la música occidental… bueno, en realidad hay excepciones, pero no nos interesan demasiado para este tema, aunque bien podrían ser tema para otro artículo. Así pues, usted es libre de elegir la frecuencia de la4, sea 440 Hz, 442 Hz, 435 Hz, como quiera. Pero una vez elegido ese valor, no puede decidir qué frecuencias tendrán las demás notas. Una ley matemática lo decidirá por usted.
Las notas musicales corresponden pues a ciertos números dependiendo de las relaciones entre ellas, y de todas con la4. Por lo tanto, casi cualquier cosa que pueda expresarse mediante números puede ser convertida en música. Pero no sin hacer algunas trampas.

Haciendo magia con los números
Cuando se publican encuestas electorales se habla mucho de la «cocina». Los datos en bruto que recogen los encuestadores son procesados según ciertos criterios supuestamente científicos, para que el resultado se ajuste en lo posible a la realidad. O más bien a lo que querrá publicar el director del periódico de turno. Pues bien, cuando usted convierte algo no musical en música, necesitará también de algún trabajo de cocina previo. Porque Júpiter no flota emitiendo un hilo musical cual ascensor. Si va usted a Júpiter, todo lo que oirá será el estruendo de sus enormes tormentas. Y si conecta un receptor de radio, tampoco escuchará músicas, sino unas emisiones caóticas. Pues bien, si convertimos estas emisiones en música directamente, no sonarían como el vídeo que vimos antes, sino más bien como cuando usted llama por error a un fax.
Usted quiere convertir el estampado de sus cortinas en música. Puede hacerse. No es que esto dijese mucho de su sentido de la poesía, pero puede hacerse. Usted decide, por ejemplo, que la frecuencia cromática de cada estampado de la cortina será traducida a frecuencia sonora. La combinación de todas esas frecuencias sonoras extraídas de colores conformará su Sinfonía de las Cortinas. Parece fácil. Consiste en convertir unos números en otros. ¿El problema? Que las relaciones numéricas entre las frecuencias de los colores no se corresponderán con las que definen los intervalos entre las notas musicales. Recordemos que se trata de una cortina. De la mercería de su barrio. Le diría, y creo que no me equivoco, que es bastante normal que su cortina con estampado de geranios no cumpla con las leyes matemáticas de la escala musical. Pero aun así, usted quiere componer su Sinfonía de las Cortinas. Y qué demonios, está en su perfecto derecho. Si Kenny G. puede hacer música con estampados de flores, ¿por qué usted no?
Así pues, si usted quiere traducir los colores a sonidos y además quiere que suene bonito, necesita hacer ese trabajo de cocina. Necesita «redondear» las cantidades de las frecuencias cromáticas para que se ajusten a los intervalos númericos musicales que suenan bien. Para entender esto, imagine que las frecuencias de las notas musicales son múltiplos de 10 (esto no es así, pero sirva para el ejemplo). En este caso, las notas musicales que suenan bien tendrían por ejemplo frecuencias de 10 (do), 20 (re), 30 (mi), y así sucesivamente. Pero las frecuencias de los colores de su cortina son 38.7, 89, 61.5. Si utiliza esas cifras directamente, su Sinfonía de las Cortinas sonará desafinada y hará que los gatos de su barrio crean que finalmente ha estallado la tan esperada revolución antihumana. Antes que nada, necesitará redondear esas cantidades, por lo que 38.7, 89, 61.5 se convertirán en 40, 90, 60. Así, tendrá usted intervalos musicales válidos, relacionando notas y colores de manera similar a como hizo el compositor ruso Alexander Scriabin. Finalmente tiene una pieza musical compuesta a partir de los colores del estampado, que no será una traslación completamente exacta pero sí lo bastante representativa como para llamarla, con mucho orgullo, la Sinfonía de las Cortinas. De este modo, puede componer una sinfonía a partir de cualquier lista de números, desde los resultados la lotería de Navidad al historial de puntuaciones de Pau Gasol, pasando las cantidades diarias anotadas en las libretas de Bárcenas. Déjese llevar.
Pero cuando las cifras se presentan en forma de lista, quizá no desee que suenen una a una, en plan tono de móvil, porque quedaría una melodía demasiado desnuda. Puede enriquecer el conjunto añadiendo notas de acompañamiento según las bien conocidas leyes de la armonía. Estas notas de acompañamiento ya no salen de la lista original de números (aunque podrían), sino que son otro trabajo de cocina cuyo interés musical dependerá de la habilidad y buen gusto del arreglista en cuestión. Después, le queda decidir qué instrumentos o qué sonidos sintetizados deben convertir la composición en un sonido físico. Después de todo este trabajo de cocina, tendrá algo muy parecido a una pieza musical convencional. Todo lo que necesita hacer es elegir su lista de cifras o su fuente de frecuencias, transformarlos en notas musicales y hacer un trabajo de cocina razonable para que el resultado sea interesante.
Si prefiere trabajar sin números, puede utilizar esas distintas fuentes para crear impulsos eléctricos y dejar que un ordenador cree la música por usted, bajo ciertos criterios programados de antemano. Ya no hay límites. El universo entero podrá ser música. Ahora todo depende de su imaginación.
A qué suenan las cosas
Muchos compositores han experimentado con este tipo de cosas. No necesariamente con las cortinas, pero sí con fuentes de inspiración de lo más extraño. Al principio hablábamos de Júpiter, y otras músicas astrales optan por sonidos más ambientales, no tan melódicos, como una representación sonora de las ondas de radio emitidas por nuestro planeta, llamada «La voz de la Tierra». El proceso es el mismo, aunque se opta por algo menos musical y más evocador de los efectos sonoros que, sobre todo debido al cine, asociamos al espacio exterior.
Pasemos a los números como tales. No esperen que distintas piezas musicales se parezcan entre sí aunque usen la misma secuencia numérica como inspiración. El resultado depende mucho de cómo decida cada compositor traducir los números a música. Unos los convierten directamente en notas, otros los usan como patrón rítmico, o como esqueleto de la estructura general para dividir la pieza en secciones. Hay muchas maneras de hacerlo. Incluso de manera conceptual o filosófica. En su día hablamos de cómo John Coltrane usaba el cuatro como número central de su gran obra, A Love Supreme, por motivos religiosos. Hay otros ejemplos similares. Por supuesto, el número áureo o proporción divina también puede usarse para hacer música, aunque algunos necesitan hacer un trabajo de cocina digno de Alberto Chicote, que de tan trabajado le quita todo misterio hasta terminar pareciendo la banda sonora de Amelie. O bien deciden convertirlo en heavy metal y añadirle una letra con frases como «geometría demoníaca»… Sí, porque los niños aficionados a la geometría son los más temidos en cualquier recreo. En cualquier caso, y esto apenas sorprende, el número áureo produce los mejores resultados cuando lo aplica un compositor realmente talentoso, como Erik Satie, quien realmente sabe aplicar esas relaciones numéricas de forma hipnótica. En cuanto a la célebre secuencia de Fibonacci, también ha sido utilizada varias veces en la música profesional. Béla Bartók abrió el tercer movimiento de una de sus composiciones con un xilófono que tocaba una nota en una cadencia inspirada por dicha secuencia. Se trata solamente de los primeros segundos del movimiento, pero resulta fascinante oírla convertida en música. Y el resto de la pieza merece mucho la pena. Este tipo de alusiones numéricas han aparecido en obras de muchos compositores, empezando por Mozart.
Siguiendo con los números, el azar es otra rica fuente de inspiración, y puede obtenerse mediante medios electrónicos o puramente físicos. John Cage usó el azar numérico para componer algunas piezas. El resultado, claro, suena bastante caótico, pero aunque de primeras pueda no producir esa impresión, no se oye exactamente lo mismo que escucharía si alguien aporrease un piano sin sentido alguno. Aquí el trabajo de cocina es mínimo, pero lo hay, y el azar no es equivalente de completo caos. Por supuesto, la electrónica proporciona la capacidad infinita de generar números aleatorios, pero también existen instrumentos que crean música aleatoria automáticamente, gracias a su mera configuración mecánica, aunque a veces suenen como C3-PO subiendo las escaleras de su casa en plena borrachera.
Siguiendo con los números, ¿qué tal convertir los decimales del número pi en una canción? Los decimales de pi conforman la melodía principal, y añadiendo otras notas para crear armonías el resultado puede ser muy parecido a una composición convencional. Incluso demasiado parecido, si se hace con más pericia que originalidad. Aunque el resultado pueda sonar sorprendente, no requiere más que aplicar ciertas reglas básicas de armonía para construir acordes en torno a las notas que representan los sucesivos decimales, un poco en plan Lego. Cualquier músico con una cierta formación puede hacer música audible con decimales. Lo difícil es conseguir que suene como la de Erik Satie.
Pasemos a algo que no consiste exactamente en números pero se le parece bastante, el ajedrez. Curioso es el trabajo de este bloguero, que un buen día quiso responder a eso que todos nos hemos preguntado alguna vez mientras esperamos nuestro turno en la cola del banco para que nos cobren una comisión por consumir oxígeno: ¿a qué suena una partida de ajedrez convertida en música? Bien, esta peculiar ocurrencia tiene su respuesta en conversiones a sonido de partidas de Bobby Fischer o de la famosa «Partida inmortal» que aparecía en una escena de Blade Runner. De manera más bien poco inesperada, el ajedrez parece sonar a jazz ambiental propio de café-bar cultureta. Y aunque no sé si el ajedrez entra en la categoría de idioma, un texto sí, y usted mismo puede componer música a partir de un texto en esta página. Pero hágalo con precaución. Yo probé tecleando la frase «sigo esperando a que Scarlett Johansson me invite a una cerveza» y la melodía resultante sonaba como Björk desangrándose en una cuneta. También hay otras muchas aplicaciones que traducen imagen a sonido, aunque por lo general de manera bastante mecánica. Algunas incluso le permiten transformar dibujos hechos por usted en mensajes musicales aptos para comunicarse con el planeta natal de Christian Bale:
Por supuesto, el camino contrario también es posible. Antes mencionamos a Alexander Scriabin, quien relacionó música y colores. Pues bien, en la interpretación de alguna de sus obras en directo se ha jugado con este efecto. Algunos programas informáticos facilitan la conversión de música en colores, siguiendo las leyes de Scriabin y añadiendo diferentes formas visuales, y así podemos ver una imponente representación cromática de algunas de las obras del ruso.
Pasando a terrenos más místicos, se ha utilizado un dispositivo electrónico parecido a un electrodo para convertir en música los impulsos que emite una planta. Así, tenemos una planta compositora, mediante un proceso similar al de obtener música de Júpiter. En este ejemplo, resulta obvio que el trabajo de cocina fue intenso, ya que el dispositivo ha sido programado para que todo suene muy armónico y bonito, eliminando de antemano no solamente las notas disonantes, sino todas aquellas que no produzcan armonías propias de una cajita de música. Aun así, incluso tan retocada por la mano humana, no deja de ser una música cuyos derechos de autor deberían ser pagados en fertilizante (vamos, como suele pasar en el negocio musical humano). Todavía más impresionante es una especie de tocadiscos, o «tocatroncos», que lee los anillos interiores del tronco de un árbol y los transforma en notas de piano. Es como la biografía del árbol convertida en sonata. Aquí apenas hay trabajo de cocina y el resultado suena todo lo disonante que puedan suponer, pero también extrañamente solemne. Yo diría que la composición de este árbol es más respetable que algunos discos comerciales que circulan por ahí.
Una filosofía parecida a la de la música hecha por plantas puede permitir que cualquier movimiento produzca música. Puede que unos simples receptores dentro de un acuario le hagan a usted sentir como la reencarnación del propio Cage. De John Cage, quiero decir, porque supongo que Nicolas Cage metería directamente la cabeza en el agua mientras berrea alguna frase incomprensible. Todavía más extremo es un artilugio que permite producir sonido mediante movimientos del cuerpo. ¿Usan la Wii como instrumento?, se preguntará usted. No… ¡usando el puente de Brooklyn!
Y para terminar en un registro muy propio de internet… ¿Qué tal música compuesta por gatos? Bien, no exactamente… pero casi. Unos científicos de la Universidad de Winsonsin estudiaron las reacciones de muchos gatos ante una amplia selección de piezas de música convencional, para ver qué tipo de timbres y secuencias de sonidos parecen gustarles más. Con los resultados obtenidos compusieron una pieza de música convencional, pero siguiendo los patrones de aquello que los gatos prefieren oír. Esto sin duda puede considerarse lo más parecido a lo que compondrían de tener oportunidad. No les sorprenderá saber que los oyentes felinos prefieren fraseos que recuerdan a los maullidos, al piar de los pájaros o al ronroneo. El resultado es algo menos bailable que Kool & the Gang, por no decir que es más aburrido que una siesta de Enya, pero a los gatos parece gustarle un montón.
Lo cierto es que aunque algunos felinos parecen tener vocación musical, no son demasiado talentosos y solamente saben tocar la misma nota todo el tiempo. Eso sí, actitud no les falta, como a este Jerry Lee Lewis en versión felina. Aunque el auténtico saber hacer pianístico, amigos, no está en los gatos, que ya hemos visto que prefieren una música monótona y poco creativa. El verdadero genio musical del reino animal es el erizo. Vean si no a este maravilloso ejemplar de erizo compositor, que sobre una base jazz es capaz de crear fraseos dignos de Thelonious Monk. Esto, amigos, esto es talento en estado puro:
Imagen de portada: cortesía de Andrew Lucia Design.











Magnífica fuente de conocimiento este artículo… y qué impotencia la que se siente al saber que hasta a Júpiter le cuesta menos componer que a mí!
¡Excelente artículo! ¿Es suyo…?
La música es libre y no debería regirse por la aplastante lógica de las matemáticas. Eso o todos somos autómatas. No me quiten eso también, era todo lo que tenía.
Ah, ¿entonces está usted como yo? ¿Sexo tampoco?
Disculpa, pero vas un poco desfasado, la relacion entre musica y matematicas es mas vieja que el baul de la Piquer, y eso de que «es libre» es mas falso que Judas, la musica y el arte en General siempre las han tenido, para bien o para mal.
Te recomiendo que leas algo sobre musica, las escalas, los modos, los tonos, la armonia, son matematicas y reglas, mucho Antes que tu y yo nacieramos.
Me temo que eres tú el que está desfasado: estás hablando exclusivamente del sistema temperado; o sea, de menos de cinco siglos y exclusivamente de la música culta occidental. Pretender reducir toda la música a eso es como reducir las matemáticas al libro de texto de 1º de la ESO.
No es el sistema temperado. Los modos, escalas y tonos ya eran viejos cuando Pitágoras descubrió las relaciones matemáticas de la armonía. En todas las culturas que practican la música o el canto existe una escala tonal y por lo tanto matemática, aunque no sea siempre la misma. La única excepción son, precisamente, las atonalidades de la música culta occidental del siglo XX.
Te han dado un buen zas en toda la boca, no sere yo el que encima haga sangre, pero es que ademas las reglas de la musica abarcan mucho mas alla que la mera armonia, los modos y escalas de cualquier cultura Musical del mundo o la llamada musica culta occidental, sino en otros muchos estilos musicales nuestros, como el Flamenco, por ejemplo. Los llamados Palos (modos que diria un academico) son patrones (reglas), de tono y armonia que un buen gutarrista y cantaor debe conocer. El arte libre es un invento de hace cuatro dias de los presuntos vanguardistas, pero que no se sostiene por si mismo, como la historia del arte ha demostrado, pero ese es otro tema.
«A diferencia del lenguaje verbal, el lenguaje musical está sujeto a leyes numéricas rígidas.»
Para nada. La música es un constructo cultural, al igual que el lenguaje hablado, una serie de convenciones sobre cierto sustrato físico y neurológico en realidad bastante maleable.
Precisamente la existencia de innumerables sistemas de afinación, tanto en la cultura occidental como en otras, muestran que las relaciones matemáticas de las alturas de las notas no necesitan ser particularmente estrictas. El sistema temperado es un ejemplo paradigmático de componenda entre una consonancia aproximada y un determinado conjunto de posibilidades combinatorias que favorecen incorporar al lenguaje ciertos giros sintácticos, como la modulación.
También se pueden oponer a esta afirmación tradiciones musicales como el gamelán indonesio o aquellas que no hacen un uso de la altura musical definida.
¡Eeeehhhvengaya, el Apichatpong Weerasethakul este, conyo…!
¡Joder! ¡Lo has escrito bien, Isobel! ¡¡Me troncho!!
Le digo lo mismo que al lector de más abajo: la tonalidad/atonalidad no era el tema del artículo y entrar en ello hubiese complicado innecesariamente el texto.
En cuanto al gamelán, no soy un experto, pero si hacemos caso, por ejemplo, a Debussy, tiene sus propias leyes armónicas. Lo que he escuchado no sigue la estructura tonal occidental, desde luego, pero está muy lejos de sonar anárquico.
Y una cosa más: podría discutirse mucho sobre el que un «sustrato físico y neurológico» sea maleable signifique también que, en ausencia de influencia moldeadora, no posea propensión hacia determinados esquemas. Eso sería mucho decir.
Por supuesto que tiene propensión hacia algunos esquemas: la psicoacústica viene aceptando desde hace tiempo que la sensación de consonancia está relacionada con la serie armónica, entendida como coincidencia o refuerzo de parciales. Pero esta consonancia psicoacústica: 1) tiene amplísimos márgenes de tolerancia, demostrados por el sistema temperado 2) no tiene necesariamente que evolucionar hacia un elemento sintáctico del lenguaje, como demuestra el gamelán. Lo que es mucho, pero muchísimo decir, es que «el lenguaje musical está sujeto a leyes numéricas rígidas», porque se está implicando una trascendencia física o matemática que no existe y se está obviando lo más importante: el carácter convencional o cultural de la música.
El sistema temperado de 12 notas, que es el que venimos utilizando en la música occidental desde hace unos siglos y es responsable de la gran mayoría de las que consideramos obras maestras de nuestra tradición, es una prueba fehaciente de que los factures culturales son más relevantes que los físicos-matemáticos-biológicos: se abandona la consonancia perfecta a favor de un sistema más favorable sintácticamente. La historia de los sistemas de afinación es la historia de la inconsistencia psicoacústica del ser humano: por un lado el oído percibe la consonancia en base a la serie armónica, que es lineal; por el otro percibe las relaciones interválicas de forma logarítmica. Esta paradoja impide que matemáticamente se pueda dividir la octava en una escala con intervalos consistentes. ¿Dónde queda entonces la trascendencia matemática de la música ;-) ?
El sistema temperado no respeta «perfectamente» la consonancia de quinta, pero las escalas occidentales se construyen, precisamente, partiendo de este intervalo. La cuestión no es que se haya renunciado a esta consonancia sino que la «resolución» del oído apenas permite percibir que en el sistema temperado no está perfectamente afinada. En cualquier caso, no se trata, de «amplísimos márgenes». Cuando uno escucha la quinta temperada (700 cents) y la contrasta con la pitagórica (702), lo que comprueba es que en realidad son casi indiscernibles.
De hecho, este sustrato físico de la música sí que existe, aunque con su margen de error (efectivamente, leyes «rígidas» tampoco aplica). Casi todas las escalas de distintas culturas respetan, precisamente estos dos intervalos: la octava (2º armónico) y la quinta (3er armónico). Incluso el tan mencionado gamelán, utiliza la 8ª y una quinta bastante desafinada, eso sí (720), al menos la escala Slendro. Por otra parte se trata de música hecha principalmente con metalófonos, cuyos espectros no son perfectamente armónicos. Esto podría haber afectado bastante al desarrollo de la propia música (¡volvemos a la física!).
En fin, que sí, que hay cultura y hay «cierto» margen. Pero también es sano divulgar (en este sentido, no creo que el artículo aspire a ser especialmente preciso) el sustrato «físico» que sostiene otros aspectos de la música más convencionales.
En ningún momento he implicado que el gamelán fuera anárquico, no sé de dónde saca eso, ni que la música no tenga reglas. Simplemente que el fundamento de estas reglas, como en toda manifestación cultural, es últimamente convencional, no trascendental. También las reglas del lenguaje verbal se pueden analizar en clave científica: por ejemplo, preposiciones, artículos o determinantes suelen ser palabras cortas por razones de optimización del soporte comunicativo. O cosas como la regla de los tres tercios en composición visual. Pero rigideces cabalísticas no, por favor, que somos bichos complejos de carne y hueso.
Lo de Pitingo me va a dejar varias noches sin dormir. La pesadilla de todo músico echa realidad. En lo demás, excelente artículo. Quizás habría que añadir que las relaciones o intervalos entre notas no son lo perfectas que parecen.
La verdad es que compadezco al guitarrista de Pitingo. Todos somos humanos y seguro que había un motivo comprensible para su error (apostaría a que el motivo pudo ser haberlo ensayado en distinto tono a requerimiento del cantante). Eso sí, lo de los gorgoritos en versión atonal es algo difícil de olvidar. Ya lo siento por sus noches de sueño. Es como haber tenido un bebé, pero sin el bebé.
Pingback: El universo es música
Con esto que cuentas una persona sorda podría oir su entorno, de tal manera que podría reconocer los objetos a su alrededor usando su oido y también claro con ayuda de un ordenador que convirtiera los objetos en sonidos.
Una persona ciega, será.
Por supuesto. Y el origen del universo no es el BIGBANG, sino una BIGBAND.
Efectivamente, como han dicho anteriormente convertir cualquier cosa que no suene a música es una chorrada.
La cagada BASE del artículo es creer que la música TONAL es la música y punto. Habla todo el rato de las CUALIDADES NUMERICAS de la música, cuando la música en sí no tiene ninguna cualidad numérica. Si la tiene la música TONAL occidental, música que, por otro lado, hace ya unos 150años que no se utiliza en música clásica contemporánea (no es algo de ayer) e incluso numerosos tipos de rock o jazz se han alejado ya de ella.
La música tonal está ordenada artificialmente, y por tanto podemos ordenar artificialmente cualquier cosa para que suene. Es estúpido. Podemos hacer la canción del «número de veces que me rasco la entrepierna al día» o la canción de «la temperatura media del agua en el caribe». Los sonidos en sí son frecuencias, por lo tanto son infinitos, y no tienen ningún orden.
Evidentemente todo esto de las relaciones matemáticas en la música es meramente cultural, a pesar de la brasa de algunos musicólogos en encontrar la «consonancia» en los intervalos matemáticos, cual Pitágoras. Si te vas a Indonesia y escuchas una orquesta de gamelanes o te vas a la selva o a la India, allí los intervalos consonantes serán otros, la tonalidad NO EXISTE, las relaciones matemáticas tampoco y el concepto de lo que suena bien y lo que suena mal se difumina para siempre.
Lo mismo ha ocurrido en nuestro país con la tonalización de todos los cantos mozárabes y antiguos que teníamos en la tradición folclórica. La capacidad de cantar y encontrar armonía en otros intervalos, muchas veces microtonales, se perdió con la introducción de instrumentos limitadísimos en este sentido como la guitarra o el piano, que solo pueden tocar en un único y exclusivo sistema de afinación Tonal.
Las «Leyes de Scriabin» que cita el autor, no son tales. Son simplemente unas relaciones que estableció debido a su sinestesia, y las cuales compartió a modo de anécdota en alguna carta con algún compañero suyo de promoción como Rachmaninov, que si bien coincidía en algunos colores, en otros no. Es bastante común en la historia musical las relaciones sinestésicas en los grandes compositores. Por otro lado, dado que mi trabajo de fin de carrera fue sobre la evolución del lenguaje musical de Scriabin, he de decir que el hombre no estaba muy bien de la cabeza. Probablemente una sífilis o alguna historia rara acabaron con su cordura años antes de morir y se dedicó a componer cientos de canciones utilizando su acorde místico por cuartas y vislumbrando representaciones de su obra en el Himalaya y cosas así. Por tanto, yo que he leído bastante sobre él, lo situaría muy lejos de alguien que relacionó matemáticas y música y más cerca de los pirados sofistas de la época. Eso sí, su evolución hasta ese punto es interesantísima musicalmente porque predice el fin de la tonalidad unos años antes que los miembros de la segunda escuela de Viena.
Ya que habla de música y mates, el autor podría haber citado a Xenakis.
Ya que nos ponemos a puntualizar:
En primer lugar, en el propio artículo se dice que incluso en la música occidental existe música que no es tonal en el sentido convencional, pero que ese no es el tema del artículo, que entrar en ello complicaría la explicación y que por eso la dejo fuera. Lo dice en el propio texto, insisto. Puedo entender que a usted le hubiese gustado que el tema del artículo fuese otro, pero no lo es. El tema elegido era más sencillo de tratar tomando como base la música tonal a la que estamos más acostumbrados en Occidente.
Ahora bien, se podría discutir mucho sobre todo lo que afirma usted sobre tonalidad. El rock, por ejemplo, nunca ha dejado de ser música tonal. En el rock existen multitud de recursos atonales, seguro, pero están casi siempre englobados dentro de estructuras tonales. Sin embargo, eso sería tema para otro artículo.
En segundo lugar, lo de calificar como «chorrada» el convertir lo no musical en musical es una valoración subjetiva que usted hace y que yo respeto pero no comparto. Piense que algunos músicos experimentan para encontrar ideas interesantes en diversas fuentes no musicales, como números, etc. Están en su derecho, y humildemente, desde mi respeto a esos músicos talentosos, no me parece una opción artística descabellada. Dependiendo de su habilidad pueden obtener muy buenos resultados mediante el «trabajo de cocina» mencionado en el artículo. Incluso de la música hecha por el azar o por un erizo pianista pueden emerger ideas interesantes (insisto: ¡el fraseo del erizo sobre el piano me parece fascinante!). La cuestión es cómo se usen después esas ideas.
En cuanto a Scriabin, bueno, sus leyes eran sus leyes y funcionaban en su sistema. Acepto enmiendas sobre la terminología, así que use la palabra que prefiera en vez de «leyes». Pero al grano: usted puede tener sobre Scriabin la opinión que quiera, pero a mí el ruso me ha servido como ejemplo para ilustrar cómo obtener una relación entre frecuencias cromáticas y sonoras. Yo personalmente prefiero escuchar a Sly Stone antes que a Scriabin, pero me temo que Sly no encajaba muy bien en la temática del texto.
O a Jimi Hendrix, que a los ingenieros de sonido les describía el sonido que buscaba hablando de colores y sensaciones visuales… pero lo hacía de una forma tan subjetiva y metafórica, sin leyes o relaciones numéricas propias, que tampoco me servía como ejemplo.
Bueno, no te ofendas por el calificativo de mi anterior comentario. Califiqué de «chorrada» simplemente el concepto de traducir valores numéricos a valores musicales. Es chorrada porque es algo tramposo y sin ningún valor. Puesto que es algo que se puede hacer con TODO en el universo. Podemos traducir pedos a colores si hacemos la relación que nos convenga. Podríamos pintar una sinfonía por ejemplo. Todo es medible por tanto todo sirve.
El problema del texto, insisto, es que la música YA no tiene en sí misma ninguna relación con las matemáticas. CERO. Ni la propia música TONAL guarda ya ninguna relación matemática perfecta que la justifique frente a otras. Hace ya 300años que se truncó la afinación (en épocas del querido Bach) para «cuadrarla» en el teclado y ayudar a los cantantes. La tercerca es el intervalo más consonante de la música occidental, ¿no? Pues no has escuchado una tercera perfecta matemática en tu vida. Y probablemente si la escuchases te resultaría disonante. Siguiendo las leyes Pitagóricas de afinación claro (que son las que siguen patrones matemáticos «precisos»). La consonancia es un hecho meramente cultural y eso está más que estudiado y no se discute en ningún lado ya.
Hay muchísimo rock NO tonal, como por ejemplo algunos tipos de math rock y algún postrock alternativo. Se utilizan hace mucho escalas exóticas fuera de la tonalidad, sonoridades orientales que no están en nuestra escala diatónica o ritmos complejos. Incluso he visto a alguno utilizar como ritmo los valores añadidos de Messiaen (básicamente copiados de la música hindú, pero que a nosotros nos resultan cacofónicos/aleatorios). Ni siquiera podemos establecer esa relación ritmo/matemáticas. Los ritmos en oriente son tremendamente complejos y muy alejados de nuestros patrones simplificados.
Que los números sean fuente de inspiración para los músicos es un tema completamente diferente; al igual que lo ha sido la religión, el amor, el drama, la naturaleza, la vida, el arte, la poesía… y así hasta el infinito. Todo puede inspirar a un compositor, incluso un erizo como bien apuntas. Hace ya más de un siglo que, con el serialismo, componer se convirtió en un ejercicio matemático más que en uno artístico, y la historia musical terminó abandonando ese camino rápidamente.
Mira que hay ejemplos en el siglo XX de músicos serialistas, serialistas integrales, minimalistas, matemáticos, etc… Insisto en que Scriabin no es el mejor ejemplo. Toda su teoría musical parte de una base filosófica sofista. Scriabin era sinestésico. Veía colores en la música cuando tocaba. Es una «enfermedad», una cualidad si queremos llamarlo así. Eso le pasa a MUCHA gente. Simplemente anotó los colores que él veía y los compartió por carta con algún amigo, de ahí que tengamos ese legado. Pero otros sinestésicos ven otros colores diferentes. Por cierto, también los falseó y exageró, nunca eran colores puros ni una imagen vívida.
Por cierto Scriabin tiene piezas preciosas, te recomiendo entero el op.16 de Preludios (de cuando adoraba a Chopin y componía a su forma pero con un rollo más oscuro) y las Sonatas 3º y 4º por ejemplo (antes de que se le fuera la pinza por completo). Aún así, de su época mística se salvan cosas, Vers La Flamme o Deux Poemes son un buen ejemplo.
Uno que descubre la musica en un vaso de agua. Cientos de años despues, la musica y las matematicas no tienen nada que ver, tendran que ver entonces con el jamon iberico, no te j…
La relacion armonica (matematica) de las Notas musicales se ha demostrado no solo teorica, sino practicamente por la ciencia. Cuando tocamos una tecla de un piano, no solo suena esa tecla, sino las adyacentes a el, por simpatia, y todas, absolutamente todas tienen una relacion armonica (frecuencia matematica con el).
Eso no es cierto. Te recomiendo leer sobre teoría musical.
Las notas ya no siguen ninguna fracción perfecta. Lo seguían en la antigua Grecia. Pero la afinación ha cambiado a lo largo del tiempo y ahora no siguen ninguna relación perfecta. Algunas perduran, obviamente como la octava y algunas quintas. Pero vamos, que la relación consonancia/matemáticas, es mentira, que es la cuestión de lo que se quería decir.
https://www.teoria.com/es/articulos/temperamentos/04-irregulares.php
Escúchate esos dos fragmentos y dime cuál suena bien. Los dos tienen los mismos «errores» repartidos en diferentes quintas. Pero tú estás acostumbrado a uno, que será el que te suene bien. Lo dicho: pura cultura.
Llevo muchos muchos años leyendo teoria Musical, y la musica tonal sigue siendo la mas usada en el mundo occidental, salvo la musica experimental y las llamadas vanguardias. La relacion consonancia matematica es cierta, y se ha demostrado fisicamente, con errores y adaptaciones, pero cierta.
Es cierto lo que dices sobre cultura y musica, pero las convenciones tonales siguen plenamente vigentes, pese a Schönberg y los que vinieron despues.
Gracias Jorge
Creo que no es del todo cierto eso de que todo el mundo sabe algo sobre música, ahí tenemos a Julio Iglesias.
Este articulo me ha puesto a tono.
Me gustó bastante el artículo, la creación sonora por medio de software está generando resultados muy interesantes. Sin meterme en la cuestión musical. El oído humano mostrará una mayor apreciación de composiciones que tienen como base un estímulo externo que se convierte en cualquier otra expresión: color, sonido, movimiento.
Lo primero felicitarte Emilio, me encantan tus artículos pero en este hay una imprecision. Los sintetizadores si que se desafínan, de hecho los modernos sintes digitales software intentan emular esa característica añadiendo un factor de aleatoriedad como un parámetro más del mismo. Gracias!
Pingback: El universo es música | Festival Internacional de Piano Guadalquivir
me parece increíble! LA MÚSICA ES EL ORIGEN DEL UNIVERSO, TODOS SOMOS MÚSICA!
EXCELENTE ARTÍCULO!!!! MUCHAS GRACIAS!!!!
TODO EMPEZÓ EN EL ESPACIO, CON MÚSICA
LA MÚSICA ES EL ORIGEN DEL UNIVERSO
TODXS SOMOS MÚSICA, ENERGÍA Y VIBRACIONES
QUE RISA LOS HATERS QUE NO ENTIENDEN ESTE ARTÍCULO Y SOLO SE PONEN A ESCRIBIR MIL RAZONES POR LAS CUALES QUERER PROBAR QUE EL ARTICULO NO ESTÁ GENIAL BUSQUEN VIDA BROS, AL FINAL TODXS SOMOS MUSICA ENTONCES NO SE ENOJEN Y ACEPTENLO!!!!
TODAS Y TODOS SOMO MÚSICA