Las preguntas de Lilia

El 18 diciembre de 2014, el profesor Paul Soler, de la Universidad de Glasgow, dio una conferencia divulgativa titulada «Neutrinos: mensajeros del espacio» en el colegio Gredos San Diego en Guadarrama (Madrid). Unos días después, recibió un correo que le escribía una de la alumnas del colegio, Lilia Cortina Fernández. El correo planteaba nada menos que cincuenta y seis preguntas (¡cincuenta y seis!), en las que Lilia demuestra, no solo una curiosidad sin límites, sino una asombrosa intuición científica.

Paul y yo somos amigos y colaboradores desde hace más de dos décadas. Trabajamos juntos muchos años en el CERN (en el experimento NOMAD, buscando oscilaciones de neutrinos tauónicos) y seguimos publicando algún trabajo conjunto de vez en cuando. En diciembre, tras su conferencia en Madrid, nos visitó en Valencia, donde formó parte del tribunal que aprobó, cum laude, la tesis del ya flamante doctor Francesc Monrabal. Paul me comentó el notable caso de Lilia y hace unos días me envió un documento con sus respuestas a la impertérrita preguntona, dejándome tan boquiabierto como sin duda se quedó él.

Paul sugirió que las preguntas de Lilia podían constituir un material interesante para publicar en Faster than light y no puedo estar más de acuerdo con él. Como el lector tendrá ocasión de constatar, el conjunto se aproxima bastante a un compendio que podríamos haber titulado: «Todo lo que usted siempre quiso saber sobre el universo pero no se atrevía a preguntar». Lilia sí se atreve y es una maravilla que lo haga. Paul, por su parte, se atreve a responder, de manera concisa y asequible, pero rigurosa. Muchas de las preguntas se refieren, directa o indirectamente a las propiedades de la luz y el año que entra (escribo estas líneas el 31 de diciembre de 2014) es el año internacional de la luz, promovido por la UNESCO. Parece apropiado que un blog que quiere moverse más rápido que la luz arranque el 2015 hablando de ella y todo lo que ilumina.

Como ya he comentado,  el enunciado de las preguntas es de Lilia y la respuesta, es de Paul. Las hipernotas son mías y expanden algunos de los temas que las preguntas van tocando. He modificado el orden original de las preguntas, para agruparlas por temáticas (origen y propiedades del universo, luz, agujeros negros).

Esta primera entrega está dedicada a las preguntas de Lilia relacionadas con la luz.

MIS PREGUNTAS SOBRE EL UNIVERSO (primera parte: LUZ)

(Preguntas:  Lilia. Respuestas: Paul Soler. Edición e hipernotas: J. J. Gómez-Cadenas)

El día que consigamos viajar a la velocidad de la luz, ¿nuestra masa será la misma de la que tenemos cuando viajamos a una velocidad normal o no tendremos masa?

Nunca podremos viajar a la velocidad de la luz. La teoría de la relatividad nos dice que para que un objeto con masa pueda viajar a la velocidad de la luz se necesita infinita energía, lo cual es imposible. La consecuencia es que solo una partícula sin masa puede alcanzar esa velocidad. Lo que sí es posible, a priori, es viajar a velocidades cercanas a la de la luz, invirtiendo, eso sí, mucha energía en ello. Por ejemplo, en el LHC[i] los protones se aceleran a una energía de 7 TeV y viajan a 0.999999991022 de la velocidad de la luz.

Si el tiempo depende de la velocidad del observador, cuando el observador va muy deprisa, ¿el tiempo pasa más rápido para él, y a su vez transcurre más tiempo? ¿se podría afirmar que mediante el proceso mencionado anteriormente seríamos capaces de comprimir el tiempo?

Hay que definir dos observadores, uno estacionario con respecto a un sistema de referencia y otro que se mueve con una velocidad (por ejemplo, en una nave espacial) con respecto al estacionario. Dentro de cada sistema de referencia nos parece que el tiempo corre igual (porque el tiempo que percibimos nosotros es siempre el tiempo en nuestro sistema estacionario). Pero desde el punto de vista del observador estacionario, para el que se mueve con una velocidad alta en la nave espacial, el tiempo se dilata. Es decir, el tiempo no se comprime sino, al contrario, el tiempo se dilata para el observador que se mueve a una velocidad alta, mientras que es el espacio el que se comprime.

Si viajamos por el universo aparentemente en línea recta y viéndonos desde nuestro punto de vista, ¿de qué forma es la trayectoria que seguimos realmente? Y si nos ve alguien que está frente a nosotros, ¿cómo nos ve llegar?

Un objeto viaja en línea recta a menos que exista una fuerza que modifique su trayectoria. Si viajas en línea recta percibes que no hay una fuerza y tanto para ti como para un observador externo te mueves a lo largo de una línea recta.

Siempre que existe una fuerza, incluida la fuerza de la gravedad, esta modifica la velocidad. Si además la fuerza no actúa en la misma dirección del movimiento, entonces la trayectoria se curva. Siempre que dejas de ir en línea recta percibes la existencia de una fuerza. Por eso, en el AVE aunque viajes a 300 km/h solo percibes la sensación de fuerza cuando el tren da una curva. Mientras se mantiene en línea recta, sobre todo si no hay traqueteos, no tienes sensación de velocidad. De hecho, si el tren se desplazara sobre raíles magnéticos, sin ningún tipo de vaivén, no tendrías forma de saber (con las ventanillas cerradas) si estás parada o te mueven a 300 km/h (de hecho no percibes que la Tierra se mueve a unos 107,000 kilómetros por hora en torno al sol, ya que, aunque la trayectoria que sigue es una elipse, la distancia que recorre nuestro planeta en su órbita es tan grande, que en la práctica, la fuerza que experimentamos debido a la curvatura es imperceptible)[1].

¿Los campos gravitatorios modifican a la luz?

Los campos gravitatorios modifican el espacio-tiempo alrededor de la masa que causa el campo. Como la luz viaja en línea recta en el espacio-tiempo, si este se curva debido al campo gravitatorio, entonces la luz también se curva aunque su velocidad siga siendo la misma.

¿Cómo afecta la gravedad al tiempo?

La teoría general de la relatividad asegura que existe una dilatación del tiempo debido a la gravedad. Es decir, para un observador cerca de un campo gravitacional grande, el tiempo transcurre más despacio que para un observador que está lejos de dicho campo. El factor de compresión es:

donde R_s es el llamado radio de Schwartschild[2] y R es el radio donde está el observador. Por ejemplo, si un planeta está a un radio que es dos veces mayor que el radio de Schwartschild, (es decir, cerca de un agujero negro)[3], entonces:

Eso quiere decir que para un observador cerca del agujero negro pasa un año, pero para el observador lejos del agujero han pasado 1.41 años. Los que están muy lejos del agujero negro envejecen más rápido que los que están cerca del agujero negro.

¿El espacio se modifica con la presencia de masa? Si es así, ¿la realidad que percibimos es una realidad distorsionada?

Aplica la respuesta a la pregunta anterior. La masa causa un campo gravitatorio que hace que se distorsione (se curve) el espacio y el tiempo alrededor de él.

¿Por qué vemos la luz?

Ves la luz porque esta interacciona con la materia a su alrededor a través de interacciones electromagnéticas. Por ejemplo, si tú ves algo es porque la luz interacciona con tu ojo en ciertas frecuencias entre 400 nm y 800 nm (es decir, entre el azul y el rojo, las frecuencias de luz visible). Aunque la luz no tiene masa, tiene energía que se traduce en su longitud de onda (mientras mayor sea la energía, menor es la longitud de onda). En resumen, vemos la luz porque tiene energía.

¿Existe la posibilidad de observar la luz en reposo?

La luz nunca puede estar en reposo, pues siempre viaja a la velocidad de la luz en el medio en el que está (en agua, por ejemplo, la luz viaja al 75% de su velocidad en el vacío). Para repetirlo una vez más, la luz siempre está en movimiento y sigue una trayectoria recta, a menos que se curve por interacciones con un medio. Por ejemplo, unas lentes de gafas tienen una cierta curvatura y hace que la luz cambie de dirección (un fenómeno que se llama refracción) dependiendo de la forma de la lente y del índice de refracción del medio (en unas lentes normales de cristal, el índice es n=1.5, que significa que la velocidad de la luz en el cristal es el 1/1.5 =67% de la velocidad de la luz en el vacío).

¿En qué punto perdemos la posibilidad de visualizar objetos que desprenden luz? ¿Depende esto del espacio que hay desde nuestra capacidad visual hasta el punto de emisión que el objeto desprende?

Mientras más lejos estemos de un objeto que emite luz, se verá con más debilidad. La relación entre la intensidad de luz emitida y la intensidad que se observa a una distancia es proporcional a la inversa de la distancia al cuadrado. Es decir, si doblas la distancia a un objeto, la intensidad de la luz disminuye a la cuarta parte. Al final, la capacidad que tienes para ver algo muy lejano depende de la capacidad de la instrumentación que uno tiene. Los astrónomos modernos usan unos detectores de luz con una gran sensibilidad que pueden observar solamente un fotón. Si la atenuación es muy grande y hay menos de un fotón entonces no se podrá observar. Los telescopios modernos tienen unos espejos enormes (por ejemplo de un diámetro de ocho metros) que intentan concentrar todos los fotones del espejo en estos detectores muy sensibles y así poder captar el máximo número de fotones provenientes de galaxias lejanas.

¿Está el pasado, presente y futuro en un mismo espacio?

Para cada punto en el espacio existe una trayectoria de tiempo, llamada línea de universo, donde existe el pasado, el presente y el futuro.

[1] Todo lo que usted siempre quiso saber sobre dinámica se cuenta con detalle en la excelente web: http://web.educastur.princast.es/proyectos/fisquiweb/Dinamica/index.htm

[2] http://es.wikipedia.org/wiki/Radio_de_Schwarzschild

[3] El radio de Schwarzschild para la masa del Sol es de 3 km mientras que el radio de Schwarzschild para un objeto de la masa terrestre sería de tan solo 8,8897 mm. El radio de Schwarzschild para el agujero negro supermasivo del centro galáctico es de aproximadamente unos 7,8 millones de kilómetros.

[i] Las siglas de Large Hadron Collider, el gigantesco acelerador de partículas que en la actualidad opera en el CERN y merced al cual se ha descubierto el bosón de Higgs.

NOTAS

Línea de universo

En física llamamos línea de universo de una partícula elemental a la secuencia de sucesos en el espacio-tiempo que se corresponden con la historia de esa partícula. Es decir, una línea de universo es una curva en el espacio-tiempo en la que cada punto puede describirse con la posición de la partícula en un tiempo concreto (x,y,z,t), donde (x,y,z) representan las tres coordenadas espaciales y t el tiempo. Por ejemplo, la órbita de la Tierra en el espacio es aproximadamente un círculo. La tierra vuelve cada año al mismo punto en el espacio. Sin embargo, en el espacio tiempo, la trayectoria de la Tierra es una hélice, ya que aunque la tierra pasa por los mismos puntos (x,y,z) cada año, lo hace en tiempos (t) más tardíos. De hecho, las líneas de universo son una manera general de representar una sucesión de eventos y su uso no está limitado a la física. Por ejemplo, una vida humana puede representarse como una línea de universo que describe completamente la historia de esa persona desde el nacimiento hasta la muerte.

Luz

En lenguaje corriente llamamos luz a una pequeña parte de las ondas electromagnéticas que llenan nuestro universo, en concreto a aquellas cuya longitud de onda está comprendida entre 400 y 700 nanómetros.

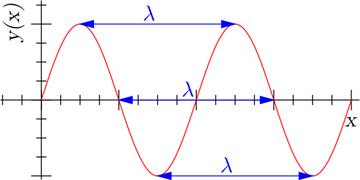
La longitud de onda es una propiedad esencial de las ondas, que ilustramos en la figura 1. Mide la distancia entre dos crestas (o dos valles consecutivos).

 

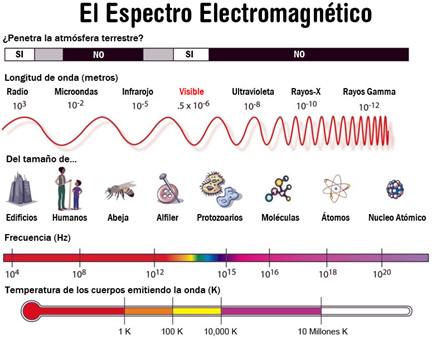
Las ondas electromagnéticas se caracterizan por su longitud de onda, tal como puede verse en la figura 2.

Como puede verse, la única diferencia entre las ondas de radio (cuya longitud de onda está comprendida entre los 10 milímetros y los 10.000 kilómetros) y la luz visible (cuya longitud de onda varía entre 400 y 700 nanómetros, esto es 4 x 10^-7 y 7 x 10^-7 metros) es lo «comprimidas» que están (la distancia entre picos). De hecho, para que un objeto sea «visible», la longitud de onda de la radiación que lo ilumina tiene que ser, como máximo del orden del tamaño del objeto (en otro caso, el objeto «cabe» entre los picos de la onda y por tanto pasa «desapercibido»). La luz visible, por tanto, nos permite resolver objetos del tamaño de milésimas de milímetro, o décima de micrómetro, entre los cuales se incluyen las bacterias (0,5 a 5 micrómetros), pero no los virus, que son demasiado pequeños (ver Figura 3) y necesitan, para resolverse una longitud de onda más pequeña que puede conseguirse con un microscopio electrónico[1].

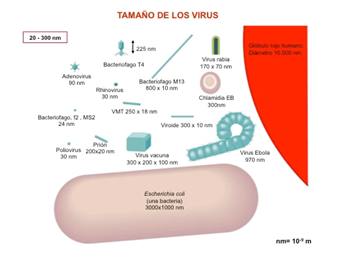
Fotón

La física cuántica asegura que las ondas electromagnéticas (y en particular la luz) están compuestas de paquetes discretos de energía, llamados fotones (del griego, phos, o sea luz). El fotón no tiene masa y por tanto viaja en el vacío con una velocidad constante, a la que denominamos c (la velocidad de la luz, aproximadamente trescientos mil kilómetros por segundo). El fotón presenta tanto propiedades corpusculares como ondulatorias. Se comporta como una onda en fenómenos como la refracción que tiene lugar en una lente, o en la cancelación por interferencia destructiva de ondas reflejadas; sin embargo, se comporta como una partícula cuando interactúa con la materia para transferir una cantidad fija de energía, que viene dada por la expresión:

donde h es la constante de Planck, c es la velocidad de la luz y  es la longitud de onda. La energía de los fotones de luz visible es de alrededor de 4×10^–19 J (o alrededor de 3 eV). Esta energía es suficiente para excitar un ojo y dar lugar a la visión.¹

Unidades de energía

El electronvoltio (símbolo eV) es una unidad que los físicos utilizan para describir la energía de los procesos atómicos. Corresponde a la variación de energía que experimenta un electrón al moverse a través de una diferencia de potencial de 1 voltio.

¿Cuánta energía mide 1 eV? Para hacernos una idea, vale la pena empezar con un ejemplo familiar. Imaginemos al joven Isaac Newton rascándose el cogote después de que una manzana, que acaba de soltarse de la rama de un árbol, le propine un capón en plena testa (de acuerdo a la leyenda, el futuro gran hombre cae en ese momento en la cuenta de que la fruta cae debido a la acción de la gravedad). Newton se dice a sí mismo:

«La masa de la manzana que acaba de caerme en la cabeza es de 100 gramos (0,1 kg). Mientras caía y debido a la acción de la gravedad, ha ido acelerando (esto es, ganando velocidad) a razón de unos diez metros por segundo, cada segundo. Es decir, la aceleración de la gravedad es g = 10 m/s². La fuerza con que la gravedad tira de la manzana es el producto de su masa por la aceleración de la gravedad, esto es, F = mg.  La masa de la manzana en kilogramos es 0,1 y por tanto:

F= 0,1 (kg) x  10 (m/s²) = 1  kg m/s². Como acabo de descubrir todo esto, creo que es justo llamar “Newton” a esta fuerza».

Por tanto:

            1 Newton = 1 N = 1  kg m/s².

Y como hemos visto, se corresponde a la fuerza con que la gravedad tira de un objeto de 0,1 gramos[2].

La unidad de energía en el sistema estándar de unidades o SI (de sus siglas en inglés) es el Julio, que se define como la cantidad de trabajo realizado por una fuerza constante de un newton para desplazar una masa de un kilogramo, un metro de longitud en la misma dirección de la fuerza. Ahora bien, si nos imaginamos que la rama de la que ha caído la manzana se encuentra a un metro del suelo, entonces para llevarla de nuevo hasta la rama, Isaac tiene que realizar una fuerza constante de 1 N (oponiéndose a la gravedad que la ha hecho caer), sobre un objeto de 0,1 kg.  El trabajo que tiene que realizar para levantar la fruta de nuevo hasta la altura de 1 metro es por tanto de 0,1 Julios (o 10^-1 J en la compacta notación de la física). O en otras palabras, 1 Julio es el trabajo que tenemos que realizar para levantar una cesta de diez manzanas (cuyo peso sería del orden de 1 kg) a 1 metro de altura.

Pues bien, el electronvoltio es una fracción diminuta de esta energía.

1 eV = a 1,6 × 10^-19 J.

No obstante, el eV es la unidad apropiada para describir las energías asociadas a los procesos atómicos. Por ejemplo, el átomo de hidrógeno consta de un solo protón alrededor del cual orbita un solo electrón. La energía necesaria para ionizar un átomo de hidrógeno (esto es, para arrancarle el electrón) es de 13,6 eV, es decir:

Energía necesaria para ionizar 1 átomo de hidrógeno = 13,6 x 1,6× 10^-19  J =21,8 × 10^-19 J.

¡Es decir, una fracción ridícula de la energía que necesitamos para levantar una manzana a un metro de altura! Por otra parte, la materia contiene una cantidad enorme de átomos. Concretamente, en 1 gramo de hidrógeno hay unos 6 x 10²³ átomos de hidrógeno. Por tanto la energía que necesitamos para ionizar un gramo de hidrógeno es 21,8 x 6 × 10^-19x 10²³ = 1,3 10⁶ J

¡Un millón de Julios! O lo que es lo mismo, diez millones la energía necesaria para levantar nuestra famosa manzana.

Todas las unidades de energía pueden relacionarse entre sí. Por ejemplo, podemos relacionar el Julio con la célebre kilocaloría cuyo consumo restringen las dietas de adelgazamiento a las que todos tendremos que someternos a la vuelta de las vacaciones navideñas.

1 J = 2,39 x 10^-4 kcal. 

De ahí podemos deducir que levantar una manzana a un metro de altura (0,1 J o 0,0000239 kcal) no consume demasiadas calorías (en las comilonas de fin de año, quien más, quien menos, se mete entre tres y cinco mil kilocalorías diarias entre pecho y espalda). Sin embargo, para ionizar 1 gramo de hidrógeno necesitamos unas trescientas kilocalorías, o 1,3 x 10⁶ x 2,39 x 10 ^-4 = 3,1 x 10² kcal. Por tanto, la energía que se requiere para mantener la actividad de un hombre robusto durante toda una jornada es la misma que hace falta para ionizar 10 meros gramos de hidrógeno.

Otro ejemplo. La energía necesaria para disociar un litro de agua (por electrólisis por ejemplo) es de 15793,31 KJ, donde el prefijo K denota «kilo» (multiplicar por mil, o sea 10³). Por tanto,

Energía para disociar 1 litro de agua (formando H2) = 1,6 x 10⁷ J.

O bien, unos 4,4 kilovatios-hora (la unidad de energía que aparece en la factura de la luz).

No son pocas las veces que, en conferencias públicas sobre energía, me preguntan por la «pila de hidrógeno» como fuente de energía. Pues bien, la pila de hidrógeno no es una fuente de energía. Cierto, podemos usar el hidrógeno para almacenar la energía, pero para formar ese hidrógeno, antes hemos tenido que gastarnos energía (para disociarlo del oxígeno en el agua). Para hacernos una idea: la potencia contratada por un hogar típico en España es del orden de 3 a 5 kilovatios. Por tanto haría falta emplear toda la energía eléctrica contratada por un hogar típico, durante una hora, para disociar un litro de agua produciendo la correspondiente cantidad de hidrógeno.

¿Y cuánto hidrógeno sería? La molécula de agua, H₂O, contiene un átomo de oxígeno y 2 de hidrógeno. El oxígeno tiene 8 protones y 8 neutrones (que pesan aproximadamente lo mismo) y la molécula de hidrógeno (H₂) contiene 2 protones. Por tanto, el peso relativo del H₂ en la molécula de agua es 2/18, o 1/9, o, aproximadamente, 0,1. Un litro de agua pesa 1 kg. Por tanto, al disociarlo generamos 100 gramos de H₂ para nuestra pila.

Pero volvamos al electronvoltio y sus múltiplos. El LHC acelera los protones hasta 7 TeV. TeV son las siglas de Tera electronvoltio. El prefijo Tera equivale a multiplicar la cantidad a la que precede por un billón (o sea por un uno seguido de 12 ceros, o 10¹²). Por tanto 1 TeV = 10¹² eV = 1,6 × 10^-7 J.

Como ya hemos comentado, a primera vista, se diría que 1 TeV es una unidad de energía muy pequeña. Pero no hay que olvidar que estamos aplicando esa energía a objetos que tienen masas muy pequeñas (y que son muy numerosos). En nuestro ejemplo, el cociente de la energía necesaria para levantar la manzana desde el suelo hasta la rama del árbol y su masa es de 0,1 J/0,1 kg = 1 J/kg. En el caso del LHC, el cociente de la energía a la que aceleramos el protón y la masa del protón es casi de 7000.

En otras palabras, la aceleración que el LHC imprime a los protones es enorme, suficiente para acelerarlos hasta velocidades cercanas a la de la luz.

Factor de dilatación relativista

Como ya hemos comentado en la nota anterior, una cantidad importante es el cociente entre la masa de un objeto y su energía. Llamamos factor de dilatación relativista, g, a ese cociente.

 

Así, el factor de dilatación relativista para un protón que se mueve en el LHC es:

 

¿Por qué el nombre «factor de dilatación relativista»? La razón es que la teoría de la relatividad asegura que el tiempo medido en el sistema de referencia de un objeto que se mueve a velocidades cercanas a las de la luz (con respecto a un determinado sistema de referencia, al que llamaremos sistema del laboratorio) se dilata (en el sistema del laboratorio) proporcionalmente a ese factor.

Es decir. Supongamos un observador[3] que viaja montado a caballo de uno de los protones que circula por el interior del LHC. Decimos de este observador que vive en «el sistema de referencia propio» del protón. El observador puede medir el tiempo (t) en el sistema propio de los protones. Por su parte, un observador situado en la cabina de control del LHC (el sistema de laboratorio) mide también el tiempo en el sistema de laboratorio (t’). Pues bien, la teoría de la relatividad nos dice que la relación entre el tiempo medido en el sistema de laboratorio y en el sistema propio es:

                                 

O en otras palabras, si los protones que circulan por el LHC fueran una nave espacial, el tiempo de la tripulación pasaría 7463 veces más lento que el tiempo en el control de la misión. Un día en la nave equivaldría a veinte años en la Tierra.

Pues bien, la velocidad que adquieren los protones en el LHC se puede calcular directamente una vez que se sabe el factor .

Obteniéndose 0,999999991022 de la velocidad de la luz.

[1] http://es.wikipedia.org/wiki/Microscopio_electrónico

[2] El joven Isaac, al que le gustan los números redondos aproxima la aceleración de la gravedad, g, al valor 10 m/s². Un valor más preciso es g = 9,81 m/s² 

[3] Un observador se define como un genio, espíritu o ángel, invisible, ingrávido e insustancial, capaz de realizar medidas de tiempo, espacio u energía allá donde se lo solicitemos.