
Hace poco más de un mes, al llegar a clase, un alumno me contaba que había leído que alguien había conseguido reventar una clave RSA de 4096 bits sin más que poner un teléfono móvil cerca del ordenador y grabando los sonidos que el procesador del mismo emitía al tratar de decodificar un mensaje (no se asusten, voy a explicar qué significa todo esto más unas líneas más abajo). Tal y como está el patio, me alegró la tarde porque me pareció una noticia sorprendente y, francamente, este tipo de descubrimientos me parecen obras de arte de las que nunca aparecerán en las paredes de ninguna galería. Pero es ¡acojonante! Si bien me alegró mucho más el hecho de que Miguel Ángel, mi alumno, llegase a clase contento por haber descubierto esto mismo y lo quisiera compartir con esa señora con gafas que le explica, entre otras cosas, aritmética modular.
Esa misma tarde, en aquella misma clase, me lamentaba en plan abuela cebolleta de que este tipo de noticias tan espectaculares no tuvieran más repercusión en la prensa, toda vez que la criptografía domina nuestras vidas más que cualquier aspirante a chef de cocina, y sobre todo ahora que el señor Edward Snowden está tan de moda y ha conseguido burlar los controles de la NSA gracias a un sistema de correo, Lavabit, que no ha podido ser decodificado por la citada agencia y que, claro, como es normal, ha sido eliminado por la misma. Tonterías a la NSA, vamos hombre…
El caso es que, bueno, pensé, quizá no es que no interesen este tipo de noticias, sino simplemente, que no todo el mundo conoce cómo funciona el sistema RSA de criptografía o, incluso, no somos conscientes de la importancia de los sistemas de encriptación de información en nuestro día a día. Así que con mi vocación de maestra (o de abuela cebolleta) he decidido tratar de explicarlo un poco, con la ilusión de que todos podamos disfrutar de este tipo de descubrimientos y ¿quién sabe?, a lo mejor también sirve para evitar la masturbación. Claro que tengo que confesar que espero que el conocimiento de este método criptográfico no afecte a la vida sexual de nadie, que ya nos tienen bastante jodidos.
Vamos al lío. Advierto a mis estudiantes de que esto es un artículo de divulgación y que el rigor con el que se explican aquí las cosas no será suficiente en los exámenes. Ni mucho menos.
Sin duda, el sistema de criptografía más importante usado en la actualidad, él o alguna de sus variantes es el sistema RSA que debe sus siglas a los apellidos de sus creadores (Rivest, Shamir y Adleman), allá por 1977 en el MIT (Massachusetts Institute of Technology). Si bien este sistema ya había sido planteado con anterioridad, en 1973, por un matemático británico que trabajaba para el servicio de inteligencia británica, pero como era super secreto de la muerte, no se supo de él hasta 1997. Es lo malo de trabajar para los servicios secretos, que son secretos.
¿Qué tenía de nuevo y/o de bueno este sistema? Que no era necesario transmitir las claves para descifrar los mensajes por ningún canal de comunicación privado, como se había hecho hasta entonces. Las claves para cifrar los mensajes eran públicas, todos podrían conocerlas. Y sin embargo, se mueve. Sí, se mueve y se seguirá moviendo mientras factorizar números de una cantidad importante de cifras sea inabordable por las máquinas. Todo se basa en escoger primos muy, muy grandes, como el de aquel anuncio del zumo, pero ahora los primos son números, números enteros mayores que 1, que solo sean divisibles por 1 y por ellos 1, como, por ejemplo, el 2, 3, 5, 7, 11…
Voy a tratar, como he dicho, de explicar cómo se usa RSA para cifrar y descifrar un mensaje. Pero, antes, tengo que contarles un poco de aritmética modular, pero en fácil, ¿eh?
En realidad, todos ya la han usado alguna vez, por ejemplo, cuando miran la hora. Todos saben que si le citan a las 19 horas, tendrán que estar donde sea que hayan quedado a las 7 de la tarde, o 7 P.M. Lo que han hecho es restar 12 (las doce horas del reloj) a 19 y ya está. Aunque 7 también es el resto de dividir 19 entre 12. Ea, pues con eso se hace aritmética modular. Calcular las horas es como trabajar, como decimos los matemáticos, módulo 12. De hecho, esto lo decimos como: 19 es congruente con 7, módulo 12 y lo escribimos así:
19≡ 7 (mód. 12)
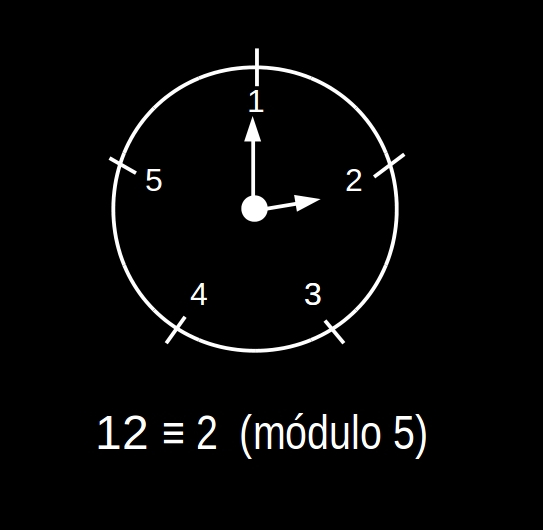
Si necesitamos trabajar con otro módulo, por ejemplo, módulo 5, lo que hacemos es pensar en un reloj que solo llegue hasta el 5. Así, módulo 5, el 12 es el 2 (o es congruente con el 2, como nos gusta decir); es como si le diésemos 2 vueltas completas al reloj y llegásemos al 2; o bien, basta con dividir 12 entre 5 y quedarse con el resto.
12≡ 2 (mód. 5)
A esto de la aritmética modular le sacan mucho partido mis hijos jugando al «Pito, pito, gorgorito». ¿Cómo? Pues simplemente, cuentan el número de «golpes’» de la cancioncita, 15 si es esta versión:
Solo queda dividir 15 entre el número de niños implicados en el sorteo y quedarse con el resto de esa división para saber cuál es la posición ganadora. Estoy segura de que los miran raro en el patio del colegio cuando confiesan que usaron aritmética modular para elegir la posición ganadora pero, oye, y la de veces que ganan, ¿eh?
Pues bien, siguiendo con la aritmética modular, con estas reglas se puede hacer eso, aritmética. Se puede sumar, restar, multiplicar… Por ejemplo, 3 más 4, módulo 5, es igual a 2, puesto que 3 más 4 es 7, y 7 es igual a 2 (módulo 5). Recuerden, módulo 5 es con un reloj que solo llega hasta el 5. Y, fíjense qué curioso, 3 por 4 es lo mismo que 3 más 4, módulo 5, claro está.
Vale, yo creo que con esto ya es suficiente para poder explicar un poco cómo funciona el sistema RSA en el cifrado de mensajes. Para ello, vamos a contarlo con una historieta. Cualquier parecido con la realidad es eso, un parecido con la realidad.
Tenemos a 3 personajes, Mariano, Luis y un tal Pedro, y unos mensajes privados que quieren enviarse entre ellos.
Lo primero que necesitamos es que cada usuario genere sus claves: una clave pública, que todo el mundo podrá conocer y una clave privada, que no debería conocer nadie.
Vamos a explicar cómo genera sus claves, por ejemplo, Luís, que es el primero en orden alfabético.
¿Cómo se hace esto? Luís elige 2 números primos muy grandes (cuanto más grandes mejor) los llamamos p y q. Por ejemplo:
p= 327414555693498015751146303749141488063642403240171463406883
y
q=693342667110830181197325401899700641361965863127336680673013.
No son suficientemente grandes, pero, bueno, nos valen para el ejemplo.
Ahora, necesitamos otro número e que cumpla unos ciertos requisitos que no vamos a explicar ahora, pero, vamos, lo más fácil es tomar como e a otro número primo, distinto de p y q.
Con estos 3 primos, p, q y e, Luís ya puede generar su clave pública: (n, e), donde n es el resultado de multiplicar p por q. Pero Luís no le dice a nadie, a nadie, quiénes son p y q, sino cuánto vale el producto de los 2.
Ya solo le falta calcular su clave privada: (n,d)
El valor n es el mismo de antes, el producto de los primos p y q. El valor d es el número que al multiplicarlo por e nos da 1, módulo (p-1)x(q-1) (ya está aquí la aritmética modular).
e x d≡ 1 (mód. (p-1)x(q-1)) (*)
Ya tenemos las claves para Luís (sus dos amiguitos las generarían siguiendo el mismo proceso): la clave pública (n,e), estará a disposición de cualquiera, y la clave privada será (n,d). Nadie debe saber cuánto vale d y, por supuesto, nadie debe saber cuánto valen p y q, ahí está la clave de la seguridad de este sistema.
Cuando Luis publica su clave (n, e), calculada como hemos dicho en el párrafo anterior, Mariano ya le puede mandar un mensaje sin que se entere el tal Pedro. ¿Cómo lo hace? Si el mensaje es, yo qué sé, «Aguanta, Luís», lo que puede hacer es sustituir cada letra por números: por ejemplo, 00 es el espacio blanco, 01 la letra A, 02 la letra B… y así, sucesivamente, como muestra la siguiente tabla:
Al sustituir cada letra por su valor («Aguanta, Luis»), quedaría (no vamos a poner la coma para que el ejemplo sea más simple)
M= 010722011421010012220920
Este mensaje, M, se agrupa en conjuntos de pocas cifras, por ejemplo, de 4 en 4 y se eleva cada uno de estos grupos al número e, pero módulo n.
Comenzando con los 4 primeros, 0107, calculamos 107 elevado a e, y nos quedamos con el resto de dividir el resultado entre n. Cuando terminamos, tenemos el mensaje cifrado, lo llamamos C,C=Me.
Para poder descifrar ese mensaje, necesitamos conocer d, la clave privada de Luís, que se supone que no conoce nadie, por lo tanto, el tal Pedro no podrá nunca interpretar este mensaje.
Pero Luís, agrupando las cifras de 4 en 4, calcula Cd y obtiene M, el mensaje sin cifrar, puesto que d y e son inversos y se cancelan.
Aquí está la gracia del sistema RSA: para descifrar cualquier mensaje enviado a Luis, es necesario conocer d. Todos saben que d es la solución de (*), pero nadie sabe quiénes son p y q, por lo tanto, no pueden plantearse resolver (*) puesto que no saben cuánto vale (p-1)x(q-1). Claro, porque conocidos p y q, calcular n es trivial, pero no al revés, si conoces solo n, tratar de calcular los 2 primos de su factorización es prácticamente imposible, incluso con las mejores computadoras. Por ahora, claro, salvo que se demuestre que P=NP.
Otro ejemplo muy, muy simple: supongamos que la clave pública de Luis es (15, 7), es decir, n=15 y e=7 (esto es una porquería de clave, ¿eh?, es solo para hacerlo más simple).
Mariano quiere mandar el mensaje CACA, primero lo transforma en números
03010301
Elige cifrarlo de 2 en 2 dígitos. Tiene que calcular 03 elevado a 7, es decir, 3 elevado a 7, que es 2187; y 2187 es igual a 12, módulo 15 (es el resto de dividir 2187 entre 15). Por lo tanto, al cifrar 03 nos quedaría 12. Al cifrar 01, nos quedaría 01. El mensaje CACA cifrado para la clave pública (15, 7) sería
12011201
¿Y bien? Pues que si la clave pública es buena, y no la de mi ejemplo, solo Luis será capaz de descifrar el mensaje, y nunca el tal Pedro, porque para descifrarlo, usará su clave privada, esto es, el número d, y eso, si hemos usados dos primos p y q suficientemente gordos (no como en el ejemplo) es prácticamente imposible. Como n=15, tenemos que n=3 x 5, por lo tanto, p=3 y q=5. Entonces, (p-1) x (q-1) = 2 x 4= 8: la d de Luis será d=7 porque 7 (que es e) multiplicado por 7 es 49 que es 1, módulo 8 (al dividir 49 entre 8, el resto es 1) . Para descifrar el mensaje cifrado, hay que elevar las cifras, de 2 en 2, de 12011201 a 7 y calcular cuánto valen módulo 15, para obtener de nuevo, 03010301 y traducirlo por CACA.
¿Se ve ahora más claro la necesidad de que los primos p y q sean suficientemente grandes para que no se pueda factorizar n?
Volviendo al principio de esta entrada,hasta ahora se creía que una clave pública de 2048 bits era suficientemennte segura. Pues bien, lo que han conseguido, entre otros uno de los padres del RSA, el que le dio la S, Shamir, es reventar una clave de 4096 bits (más de 1200 cifras) tan solo escuchando los ruiditos que hace el procesador del ordenador al encriptar el mensaje. ¡Anda que no! A mí, francamente, me parece absolutamente alucinante… Habrá que seguir buscando primos lo más grandes posibles para aumentar la seguridad de nuestras comunicaciones, sino queremos ser tan primos como para seguir usando los SMS y que todos se enteren, claro. Aunque, pensándolo bien, qué más da que se enteren de nuestros trapicheos por SMS si después siempre pueden desaparecer los discos duros que servirían para probar esas cosas que el nota dice que nunca se podrán demostrar.





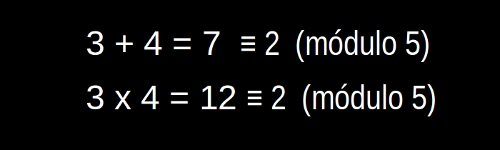










Una pequeña puntualización. Lo que ha hecho Shamir en su experimento es conseguir la clave privada, no romper el cifrado.
Gracias por el artículo.
Muchas gracias a ti.
Conseguida la clave privada, se puede romper el cifrado.
Sin la menor duda, y preguntársela al usuario es la manera más sencilla de conseguirla – y funciona en la mayoría de los casos – pero no se considera «romper» el cifrado.
Un criptosistema depende de varios elementos, no sólo del algoritmo matemático que cifra los datos. La elección de contraseñas, su almacenamiento, o vulnerabilidades del programa (recuperar información sin cifrar de la RAM) o del hardware, como en este caso, tiran por tierra la efectividad del cifrado pero no porque haya nada malo en el cifrado propiamente dicho.
¿No es lo mismo que hizo el protagonista de Juegos de guerra con una grabadora?
igual he entendido mal la frase pero, al principio cuando has dado ejemplos de números primos has puesto un 9. :S
Pequeño error en la siguiente lista dada de números primos: «el 2, 3, 5, 7,—>9<—, 11".
Sigo leyendo.
¡Ojo que el 9 no es primo y lo tienes en los ejemplos! :-)
Ops, efectivamente, se coló el 9 con los primos, ¡arreglado!
¡Muchas gracias! :)
Justo leo esto días después de haber hecho un examen de Redes de Computadores (en el cuál entraba la encriptación, claro) ¡me persiguen las claves!
Muy interesante, así como bien explicado, Clara.
Si alguien quiere profundizar, le recomiendo: https://www.coursera.org/specialization/cybersecurity/7?utm_medium=listingPage
Muy buen articulo, despierta interés por la computación y el funcionamiento de la seguridad en internet. Una pregunta, ¿Esto se puede comparar al cifrado de contraseñas personales y bancarias?
Por regla general, no. Como se puede deducir del método que ha explicado Clara, cifrar un mensaje con criptografía de clave pública es lentísimo; hay que coger el mensaje, interpretado como un número, y elevarlo a una potencia de hasta 4096 dígitos binarios.
Por lo general la criptografía de clave pública solo se utiliza para enviar información, pero nunca para almacenar información. Incluso cuando se envía información lo que se hace es cifrar la información con un algoritmo de clave simétrica (la clave para cifrar es la misma que para descifrar), que son mucho más rápidos para una seguridad equivalente, y lo único que se cifra con clave pública es la clave que se ha usado para cifrar el contenido del mensaje con el otro sistema.
Gracias por el artículo, muy ilustrativo.
Sólo una puntualización, evitemos usar «encriptación/encriptar» cuando lo correcto es cifrado/cifrar, especialmente en artículos que sirvan de referencia como éste.
Sé que la RAE lo incluirá tarde o temprano, pero la RAE hace muchas barbaridades (por lo de tomar palabras de pueblos bárbaros, claro) :-)
He venido hasta los comentarios sin leer lo demás solo para ver si alguien veía este detalle ya que me llamó la atención que ella lo hiciera.
Ahora si iré a leer.
Pingback: Snowden y sus primos
¿Qué es el arte? ¿Y tú me lo preguntas, Clara Grima? Arte eres tú.
Interesante artículo. Quisiera mostrar un pequeño apunte al respecto: La seguridad del sistema RSA descansa en el hecho de que el progreso tecnológico a la hora de factorizar números grandes (mayores que un gúgol) es lo suficientemente lento como para que un ordenador actual necesite un número de cálculos que aumentan exponencialmente con el número N que se desea factorizar, y por tanto la tarea se vuelve impracticable.
En otras palabras, la seguridad de RSA se basa en una complejidad de cálculo que no ha sido demostrada de forma rigurosa, es decir, matemática. Esto puede acarrear graves problemas cuando los ordenadores cuánticos sean una realidad (aún quedan bastantes años), pero tarde o temprano ese día llegará y para entonces el proceso de factorización será tan sencillo como la multiplicación. De ahí a que se haya estado estudiando en los últimos 20 años en lo que se conoce como criptografía cuántica, donde queda garantizada la seguridad de la distribución de claves debido a que se parte de las leyes de la mecánica cuántica y no de la vaga certeza de una complejidad computacional que imposibilite el espionaje en la práctica.
Sé que todo esto no tiene cabida en un artículo introductorio sobre el tema, pero es interesante tenerlo en cuenta de cara al futuro.
no acabo de ver por que hace falta calcular d modulo (p-1)x(q-1), pero es que soy muy burra, el inverso de e siempre podrias hacerlo con tal de que e y lo que uses fuesen primos entre si, no? (bezout dixit…)
Si Laura, el inverso siempre existiría. Pero lo que necesitas es que además el descifrado realmente descifre. Es decir, que cuando elevas el número a «d» vuelvas a obtener la palabra original.
Cuando Clara dice «e y d son inversos y se cancelan», eso en realidad tiene más miga detrás (que ella no cuenta para no sobrecargar), interviene el Teorema de Euler, y para eso necesitas que el módulo sea (p-1)*(q-1), que es precisamente la «función de Euler» de n.
Pingback: El Ministerio de la Verdad - Jot Down Cultural Magazine