Ilustración de Raquel Garcia Ulldemollins
Supongo que debería alegrarme…
No han sido pocas las veces que me he desorientado al salir del mar en una playa amplia tratando de ubicar mi sombrilla y, toda vez que no tengo ya edad de anunciarme como perdida (qué desafortunada polisemia) en la megafonía de la playa de la Victoria, por ejemplo, he optado por bañarme con unas Ray Ban, a lo Top Gun, disfrazando así de pija cool a una señora corta de vista.
Pero lo cierto es que no, no me alegro.
En un país en el que asistimos con estupefacción e impotencia a los desmadres cometidos en nombre de la monarquía o de parte de la clase política, la noticia de que el gobierno modifique la Ley de Costas para acercar la zarpa urbanística a los mares que bañan nuestras costas no puede alegrar a nadie con sentido común y/o sin intereses económicos en este business.
Claro está que en esta bacanal en la que están engullendo el sistema público de Sanidad y Educación, en la que se meten palos en las ruedas de la ciencia, se elitiza el sistema judicial, con los mejores platos, o los únicos, frente a las sillas de bancos y poderosos, puede que este hecho haya pasado desapercibido para la mayoría de la ciudadanía preocupada por conservar su puesto de trabajo, los que tengan, sus casas, los que tengan, sus ahorros, los que tengan… Por conservar lo que tengan los que tengan…
En fin, parafraseando a Umbral, D.E.P, y consciente de que este chiste no lo entienden los más jóvenes, yo he venido aquí a hablar de matemáticas, no de leyes de costas… Aunque, mira, podemos contar algo de costas y matemáticas, ¡digo!
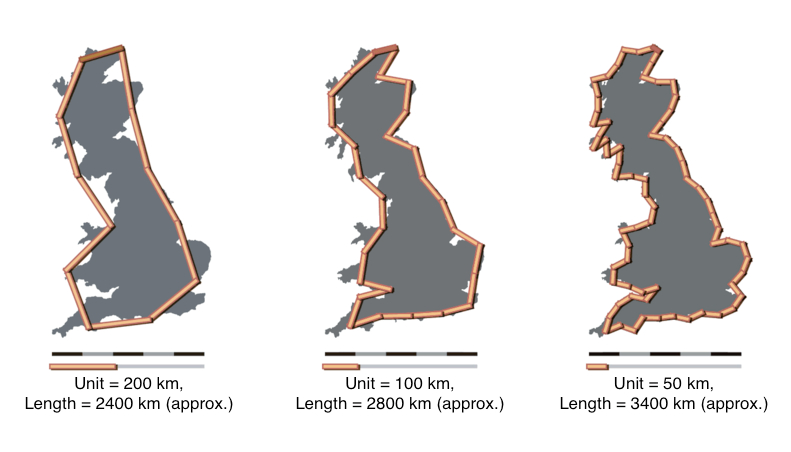
Se me ha venido a la mente un trabajo de Mandelbrot, de 1967, en el que el matemático franco-americano, nacido en Polonia, se preguntaba cuánto medía la costa de Gran Bretaña. Sí, ¿qué pasa? Los matemáticos somos así.
Tonterías aparte, lo que Benoit Mandelbrot planteaba era la siguiente, en principio, paradoja: cuanto más pequeña sea la unidad de medida usada para medir la costa, más medirá esta (me refiero a la costa, todavía me cuesta no tildar los demostrativos).
La siguiente imagen nos aclara mejor lo que quiero decir:
Según esto, uno puede pensar en que cuanto más se acerque a la costa para medirla, más kilómetros tendrá esta y, por lo tanto, más hoteles se pueden construir y que eso es lo que han interpretado las mentes preclaras de nuestro gobierno para redactar la citada enmienda. Pero no estoy yo tan segura de que se hayan leído el mencionado artículo de Mandelbrot, llámenme desconfiada…
Volviendo a la paradoja planteada por el amigo Benoit, lo que él intuía en esa observación era que existían objetos geométricos que las matemáticas aún no habían sabido describir. Esos objetos, a los que un poco más tarde el llamó fractales, eran objetos que no tenían por qué tener una dimensión entera, esto es, que no tenían que tener dimensión 0, como un punto, dimensión 1, como una recta, dimensión 2, como un plano, etc… Observó además que estos objetos, los fractales eran autosimilares, o lo que es lo mismo, que si tomábamos un trozo de ellos y hacíamos zoom sobre él, nos acercábamos lo suficiente, volveríamos a encontrar esa misma forma (la del trozo) repetida una infinidad de veces. Tratando de buscar una analogía actual, es como cuando aparece un caso grande de corrupción y nos acercamos y vamos descubriendo que, en realidad, hay infinitos casos de corrupción similares dentro del caso grande, ¿me explico?
La belleza intrínseca de los fractales y su misteriosa geometría no ha pasado desapercibida desde los trabajos de Mandelbrot y podéis encontrar, por ejemplo, entradas maravillosas y bien escritas sobre ellos, si tenéis curiosidad por toquetearlos. Permitidme que os recomiende esta de un gran amigo, a pesar de que es físico y cordobés, que lo explica muy clarito.
Dejadme solamente que no me resista a describiros uno de mis fractales favoritos (y de De Guindos, supongo, porque está hecho de recortes), en el que aúnan dos conceptos matemáticos muy presentes en la naturaleza, bastante conocidos e infinitamente bellos: el fractal de Fibonacci.
Por si a alguien no le suena Fibonacci, le diré que, aunque su verdadero nombre era Leonardo de Pisa, fue un matemático conocido, entre otras cosas, por la descripción de una sucesión numérica llamada, con muy poca originalidad, la sucesión de Fibonacci, que aparece constantemente en la naturaleza: en el número de hojas de las flores, en las espirales de las piñas… Los 2 primeros términos son 1 y 1, y a partir de ahí, los siguientes se calculan sumando los 2 términos anteriores:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …
También pueden encontrar la famosa sucesión en trabajos de Economía e incluso hay quien usa el sistema de apuestas Fibonacci para ganar algo de dinero en las mismas.
Pues bien, hallábame yo preparando una entrada para el blog de Mati sobre la anterior sucesión, cuando descubrí el objeto del que he hablado unas líneas más arriba: el fractal de Fibonacci y me pareció de una belleza tal que no he perdido ninguna oportunidad de hablar de él cuando se me ha puesto a tiro.
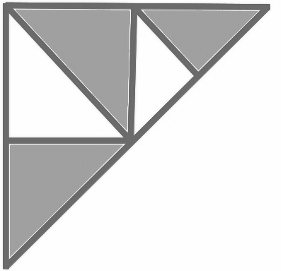
Vamos allá. Se trata de hacer los recortes con un poco de cuidado: partimos de un triángulo rectángulo, trazamos la altura desde el ángulo recto y nos quedan 2 triángulos rectángulos iguales, ¿no? En uno de esos triángulos, calculamos la altura desde al ángulo recto y recortamos una de las 2 mitades que produzca.
Se trata ahora de repetir el proceso en el triángulo sombreado de mayor área.
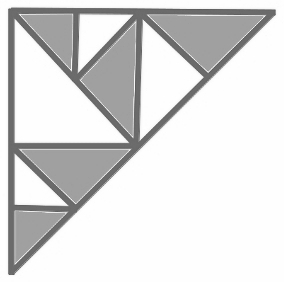
Volvemos a recortar según el método descrito en los 2 triángulos de mayor área.
Y así, sucesivamente. Lo curioso es que cada vez, el número de triángulos de mayor área que aparecen y a los que tenemos que recortar un trozo, es un número de Fibonacci.
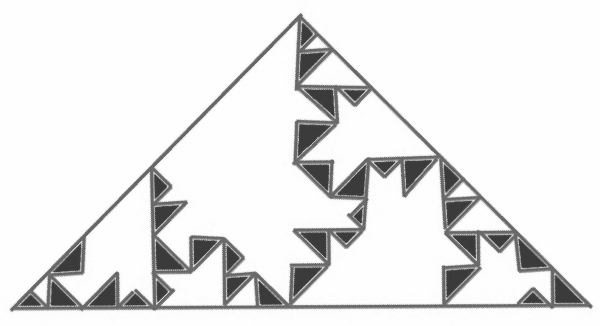
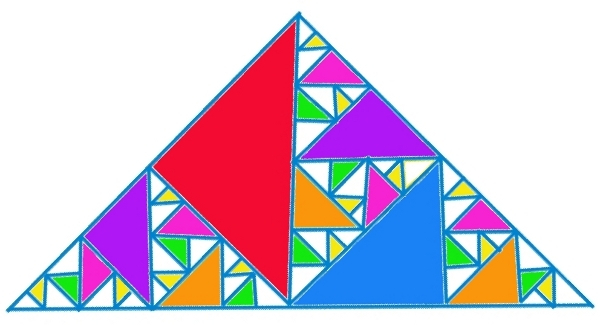
Si repetimos el proceso unos pasos más, ya nos va quedando el siguiente fractal, cada vez con menos área, por culpa de los recortes.
Este hecho, el de que en cada paso el número de triángulos susceptibles de ser recortados sea un término de la sucesión de Fibonacci por sí solo, me parece lo suficientemente atractivo; pero es que, además, si coloreamos con colores distintos los recortes que hemos hecho en el proceso, dando el mismo color a los recortes de igual área, también encontramos la sucesión de Fibonacci.
Maravilloso, ¿no creen?
Como suelo decir en estos casos, pueden llorar, yo también lloré cuando lo descubrí.
Y, qué coño, es mejor llorar de emoción en plan Stendhal que hacerlo de impotencia ante las mentiras y eufemismos de algunos. Nos están dando tantos palos por tantos sitios que ya no sabemos hacia dónde mirar. Una tiene la tentación de esconder la cabeza al estilo del avestruz. Afortunadamente, después se percata de que, aunque el ave estrucioniforme protege hábilmente la cabeza, deja el culo fuera…
Y hablando de culos fuera, espero que, al menos, no presenten ninguna enmienda a la Ley de Costas en la que también prohíban hacer nudismo porque les molesten nuestros cuerpos desnudos a menos de 20 metros, porque a 300 no vamos a tener espacio para colocarnos.














Pingback: Clara Grima: Nosotros a 300 y el mar a 20
Brillante, Clara!
Una observación y una duda:
1. Observación: aunque no lo especificas, el triángulo de partida ha de ser isósceles, además de rectángulo, de manera que la altura correspondiente a la hipotenusa sea también mediatriz y divida el triángulo en dos partes iguales.
2. Duda: A la hora de seleccionar en cada iteración el triángulo a eliminar, se hace siguiendo algún criterio (como en el triángulo de Sierpinski) o se realiza al azar de entre todos los posibles?
Si te digo la verdad no entiendo mucho de fractales y no tengo ni idea pero viendo el ejemplo yo diría que se ha realizado siempre siguiendo un criterio determinado: en este caso se divide el triángulo inicial en dos, se toma la mitad a la izquierda de la altura (si miramos el triangulo situando la base en horizontal en la parte de abajo), se divide este triangulo por la mitad utilizando otra vez la altura y se elimina el triangulo que queda nuevamente a la izquierda (no sé si me explico). Sin duda daría igual hacerlo siempre escogiendo el de la derecha, pero diría que no es posible escoger el triángulo a eliminar al azar. Yo diría que se perdería el orden y la repetición de estructuras y además existirían zonas inconexas con el resto o zonas en las que obtendrías un cuadrado (imagina que en la imagen en la que se han realizado mayor número de divisiones, la que hay antes de la imagen con colorines, cambias la división tan sólo en uno de los triángulos y observa el resultado, haz la prueba varias veces a ver qué te sale).
Por cierto, se me olvidó en la anterior entrada: excelente entrada. Un saludo.
Qué decir… ¡Enhorabuena, Clari!
Knut – Fibonacci unfolds
http://www.youtube.com/watch?v=0bSfaFv8l8c
Bueno chicos a los que os halláis leído este articulo como guinda os recomiendo este vídeo para terminar de ver como la sucesión de Fibonacci se desarrolla en la naturaleza:
http://www.youtube.com/watch?v=A1KwKkh-03c
Mejor mezcla, imposible… ¡me ha encantado!
Bueno, pero entonces, ¿cuánto mide la costa de Gran Bretaña?
Soy amigo de Raquel y sólo puedo decirte qu encuentro tu artículo muy acertado.
Lo de la medición de las costas siempre me ha fascinado, gracias a la teoría de los fractales. He llegado a pensar que la Costa Brava siguiendo el contorno de cada roca a nivel de microscopio podría tener millones de Km de longitud. El límite, en teoría, estaría dado por los átomos o por los protones, o a lo mejor, ni siquiera por ellos.
Fascinante el tema, de todas maneras…
Un saludo.
Diego
Pero supongo que de alguna forma se debe obtener una solución de compromiso. Supongo que se aplicará un modelo de costa medible de cara a calcular «cosas».
La pregunta es, ¿la matemática fractal aporta algo de cara a este modelo? ¿permite obtener un resultado más preciso para un error dado? Si simplemente nos informa de que no hay solución ¿es sólo un juego matemático del que hay que prescindir cuando queramos realmente calcular algo relacionado con la longitud de costa?
Pregunto desde la mayor ignorancia, pero también con curiosidad. Soy ingeniero aeronáutico y me gustan las matemáticas, pero nunca he visto una aplicación real de los fractales salvo en los decorados de las películas generados por ordenador. Posiblemente tenga un espíritu demasiado práctico por deformación profesional.
Diego, además la medida sería variable según la altura a la que se hicieran las mediciones… el nivel del mar varía con la marea así que… jejeje
Salu2!
Que frescas son las mates con Clara Grima!!!
Un saludo y enhorabuena por el artículo.
La mayoría de las personas no lo entienden, por tanto, como se creen más listos las engañan. El problema es que les dices que les están engañando y se quedan igual ¿vivimos con Zombies?
Sólo un detalle: en realidad los avestruces (y son LOS avestruces) esconden la cabeza únicamente cuando tienen que proteger a su nido, extendiendo las alas para parecer un árbol caído. A la carrera son más rápidos que sus posibles depredadores y pegan unas patadas y unos picotazos capaces de dejar KO a más de uno de ellos.
¿Los pronombres demostrativos no se tildan? (excepto «esto»). Es decir, éste, ésta, éstos, ése, ésa, ésos…
¿Me parece recordar que los determinantes (o adjetivos) demostrativos son los que no se tildan, no?
Magnífico artículo. Me recuerda a cuando me enseñaron en bup la existencia del infinito con un cuadrado y su diagonal, cada vez más dividida en mitades. Da igual el número de veces que dividas en (sub)cuadrados, que la distancia entre los vértices siempre es igual a dos lados. Excepto si divides en infinitos cuadrados, que la distancia es la raíz de dos.
Saludos…
Álvaro: no, creo recordar que se pasó del uso obligatorio de la tilde en el caso de los pronombres demostrativos a recomendar no usarlo y desde 2010 no es correcto tildar dichas palabras: http://www.rae.es/rae/gestores/gespub000018.nsf/(voAnexos)/arch8100821B76809110C12571B80038BA4A/$File/CuestionesparaelFAQdeconsultas.htm#novOrto5
Magnífico artículo y nos deja con ganas de más.
Es curioso, al ver la última imagen coloreada he tenido una sensación similar a la de oír una composición musical.
Si oye música con los colores,quizás sea sinestésico.
Genial.
Muy bonito.