Todos los vivos y todos los muertos

¿Tiene sentido buscar inteligencia extraterrestre? Para contestar a esa pregunta, lo primero es plantearnos si existen otras civilizaciones en la galaxia que emitan (o hayan emitido alguna vez) mensajes detectables con nuestra tecnología actual. Obviamente, si estamos solos en la Vía Láctea, SETI es una insensatez. Por el contrario, si estimamos que la galaxia está de bote en bote, sería insensato no intentar averiguar que se está cociendo a nuestro alrededor.

La cuestión, por tanto es: ¿Podemos calcular cuántas civilizaciones inteligentes, capaces de comunicarse y dispuestas a hacerlo hay en la galaxia? (Vamos a llamarlas CACs, Civilizaciones Avanzadas y Comunicativas) Ojo, esa comunicación tienen que ocurrir en un tiempo que nos permita detectar las posibles señales. Si una civilización en Alpha de Centauri (a cuatro años luz de aquí) estuvo emitiendo señales durante milenios («hola terrícolas, aquí alpha de centauri, les ofrecemos el secreto de la eterna juventud, la fórmula de la democracia universal y el antídoto para librarse de los economistas financieros, si están interesados, por favor, respondan») pero dejó de emitir hace, digamos, medio siglo, sus señales pasaron de largo antes de que nadie en el planeta Tierra estuviera escuchando (una pena). La ventana temporal, por tanto, es muy importante.

La ecuación de Drake es una sencilla fórmula que nos permite, en primer lugar plantear este cálculo (esta es la parte fácil). Utilizándola, es posible obtener órdenes de magnitud del número de CACs, pero como veremos, la incertidumbre en ese número es muy grande. La fórmula de Drake, por cierto, se llama así en honor Frank Drake, astrónomo, pionero de SETI y profesor en la Universidad de California en Santa Cruz, donde yo trabajé dos años como postodc, con una beca Fulbright (tuve la suerte de asistir a uno de sus cursos sobre SETI, que por cierto, se desarrollaba casi íntegramente en el bosque que rodea la universidad).

La fórmula en cuestión es bastante sencilla:

donde:

  Número de civilizaciones tecnológicamente avanzadas, capaces de comunicarse y dispuestas a hacerlo.

 Número de estrellas en la Vía Láctea.

 La fracción de esas estrellas que tienen sistemas planetarios.

 Número de planetas apropiados para la vida, por cada sistema planetario.

 La fracción de esos planetas donde se desarrolla vida.

 La fracción de esos planetas donde se desarrolla la inteligencia.

 La fracción de esos planetas capaces de comunicarse mediante señales de radio.

  El tiempo durante el cual la civilización emite señales al espacio.

 La edad de la galaxia.

Para entender la ecuación de Drake es necesario hacernos una idea de los órdenes de magnitud de cada uno de los factores que la componen. Lo cual, como veremos, es una tarea más difícil de lo que parece.

Empecemos por el número de estrellas que hay en la galaxia, una cantidad que se conoce con bastante exactitud. El orden de magnitud es doscientos mil millones, esto es un dos seguido de once ceros, 200000000000, o . Para hacernos una idea de lo que significa tal cantidad, podemos hacer el ejercicio de contar los granos de arena de una playa.

La que veo mientras escribo estas líneas (en Port Saplaya, cerca de Valencia), tiene alrededor de un kilómetro de largo por unos veinte metros de ancho, lo que nos da una superficie, S de:

El espesor de la capa de arena (seca) que encontramos en la playa, si empezamos a cavar, puede ser del orden de diez centímetros antes de que el hoyo se nos llene de agua. Entonces, el volumen de la playa que contiene arena seca, V (en milímetros cúbicos) es:

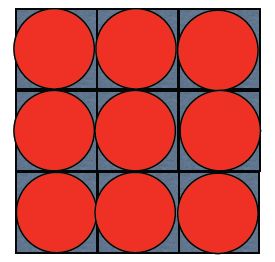
Un grano de arena es una esfera que tiene unos dos milímetros de diámetro. Por otra parte, si queremos llenar un volumen rectangular como el de la playa con esferas, tenemos que tener en cuenta que no podemos compactarlas de manera perfecta. De hecho, cada una de ellas, ocupa tanto como un cubo cuyo lado fuera el diámetro (d) de la esfera, tal como se ilustra en la figura. El volumen de dicho cubo es simplemente milímetros cúbicos.

El número de granos de arena en la playa lo obtenemos dividiendo el volumen de la playa por el volumen de los imaginarios cubos que contienen nuestros granos de arena.

Que es un número bastante cercano al que nos ocupa (de hecho, el número de estrellas en la galaxia podría ser tan algo como cuatrocientos mil millones). Resulta instructivo hacer el ejercicio de imaginarnos unos diez bulldozers recogiendo la arena de toda la playa que tengo delante y depositándola en enormes contenedores habilitados al respecto. Si tenemos curiosidad en saber cuánto pesa toda esa arena, la respuesta es bien sencilla. Un centímetro cúbico de arena pesa unos dos gramos. El volumen de arena de la playa es  centímetros cúbicos. Pesa, por tanto  gramos, o cuatro millones de kilos, o cuatro mil toneladas.

Ahora sólo nos queda contar uno a uno, cada grano de arena de esas cuatro mil toneladas, para entender la inmensidad de estrellas que pueblan nuestra galaxia. El orden de magnitud, por cierto, es el mismo que el del número de neuronas en nuestro cerebro, y también el número de galaxias en el universo.

Partimos pues de un número muy grande de estrellas. Y esto me lleva a mencionar un argumento filosófico que permea toda la búsqueda de inteligencia artificial. La idea de que no somos especiales.

Este principio de mediocridad es algo relativamente reciente. En la edad media, la Tierra era el centro del universo en torno a la cual giraban el resto de los astros celestes. No sólo eso, sino que toda la creación se supeditaba al ser humano. Los animales con los que compartimos el planeta no eran otra cosa que robots animados, puestos ahí para sernos útiles por el creador, que a su vez, entretenía su infinito ocio jugando con sus criaturas (nosotros). Así, el hombre era el centro de la creación y por ende, del cosmos.

No es de extrañar que los cardenales se negaran a mirar por el telescopio que les ofrecía Galileo. Que la luna no fuera una esfera de cristal perfecto si no un globo torturado por los impactos de los meteoritos fue sólo el primer golpe a la ilusión de hijos únicos que durante tantos siglos alimentó la humanidad. Tras Galileo vinieron Newton y Descartes, a describir un cosmos que funciona como un reloj, empujando a Dios a la categoría de relojero (hasta entonces había sido más bien el Sumo Malabarista) y a la Tierra a un astro más de un vasto firmamento.

La Ciencia del XIX y el XX ha demostrado cuán inmensamente vasto ese universo es. Hay tantas estrellas como granos de arena en una playa, pero tantas galaxias como estrellas en la Vía Láctea. Y en ese inmenso paisaje, la Tierra no es sino el tercer planeta de una estrella mediocre, en un barrio periférico de una galaxia cualquiera. En cuanto al Dios relojero, cada vez cuesta más de encajar en un universo que la física moderna describe con pasmosa exactitud hasta una fracción de segundo después del Big Bag. Y si la física ha tenido poca compasión con el Creador, la biología ha sido aún más implacable. Una de las plumas más lúcidas de los últimos años, Richard Dawkins, compara la evolución con un relojero ciego. Ciego, e insensible, habría que decir, ciertamente, sin preferencia alguna por cierta raza de peligrosos monos bípedos, que parecen sufrir de encefalitis (cien mil millones de neuronas en nuestro cerebro, tantas como estrellas en la galaxia) que les provoca una especie de locura colectiva y muy peligrosa.

La imagen que nos dibuja la ciencia no deja mucho espacio para considerarnos hijos preferidos de ninguna divinidad, ni especiales en ningún sentido. Y de ahí el principio de mediocridad que viene a decir. Si somos una raza corriente, en un planeta corriente, entonces debemos ser bastante típicos. Deben haber muchos otros como nosotros. Mediocres quiere decir, además, ni muy tontos (posiblemente haya otras civilizaciones más atrasadas que la nuestra) ni muy listos (habrá también otras mucho más avanzadas).

Pero el principio de mediocridad no es, hasta que se demuestre lo contrario, más que un prejuicio intelectual. A pesar de todo, podríamos ser los ganadores de una lotería cósmica, los primeros seres inteligentes de la galaxia (mentira: ballenas y delfines posiblemente son tan inteligentes como nosotros, sin estar tan chiflados). Para ir más allá de ideologías (muchos de los que se oponen a SETI sostienen la convicción, explícita o implícita de que seguimos siendo especiales, los hijos predilectos de la divinidad) es necesario echar unos números, como haremos a lo largo de las siguientes entregas.

He leído pero no he comprobado, otro orden de magnitud, que ofrezco, sin garantías al avispado lector, sólo por su belleza. El número de estrellas de la galaxia sería el mismo que el de personas que jamás hayan habitado el planeta, la suma de todos los vivos y todos los muertos, una estrella, por cada alma que jamás haya pisado la Tierra.